题目内容
已知函数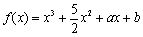 (
(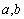 为常数),其图象是曲线
为常数),其图象是曲线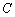 .
.
(1)当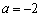 时,求函数
时,求函数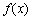 的单调减区间;
的单调减区间;
(2)设函数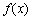 的导函数为
的导函数为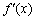 ,若存在唯一的实数
,若存在唯一的实数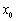 ,使得
,使得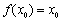 与
与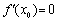 同时成立,求实数
同时成立,求实数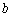 的取值范围;
的取值范围;
(3)已知点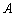 为曲线
为曲线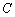 上的动点,在点
上的动点,在点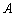 处作曲线
处作曲线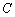 的切线
的切线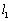 与曲线
与曲线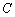 交于另一点
交于另一点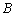 ,在点
,在点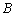 处作曲线
处作曲线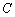 的切线
的切线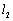 ,设切线
,设切线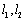 的斜率分别为
的斜率分别为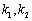 .问:是否存在常数
.问:是否存在常数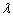 ,使得
,使得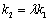 ?若存在,求出
?若存在,求出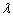 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)当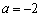 时,
时, 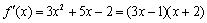 .
.
令f ¢(x)<0,解得 ,所以f(x)的单调减区间为
,所以f(x)的单调减区间为 .
.
(2) 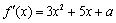 ,由题意知
,由题意知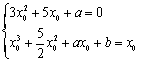 消去
消去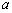 ,
,
得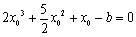 有唯一解.
有唯一解.
令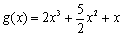 ,则
,则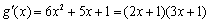 ,
,
所以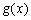 在区间
在区间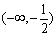 ,
,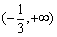 上是增函数,在
上是增函数,在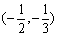 上是减函数,
上是减函数,
又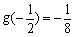 ,
,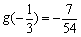 ,
,
故实数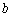 的取值范围是
的取值范围是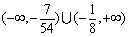 .
.
(3)设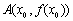 ,则点
,则点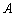 处切线方程为
处切线方程为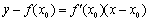 ,
,
与曲线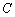 :
: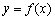 联立方程组,得
联立方程组,得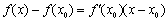 ,即
,即 ,
,
所以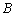 点的横坐标
点的横坐标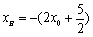 .
.
由题意知,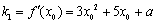 ,
,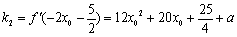 ,
,
若存在常数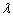 ,使得
,使得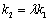 ,则
,则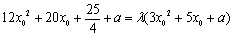 ,
,
即存在常数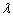 ,使得
,使得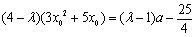 ,
,
所以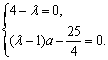 解得
解得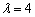 ,
, .
.
故 时,存在常数
时,存在常数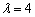 ,使
,使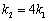 ;
;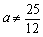 时,不存在常数
时,不存在常数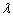 ,使
,使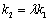 .
.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为8,则a+b的最小值为_____________.
的最大值为8,则a+b的最小值为_____________.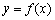 是定义在
是定义在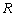 上的奇函数,且当
上的奇函数,且当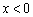 时,
时,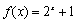 ,则
,则 。
。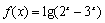 的定义域为 .
的定义域为 .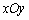 中,若动点
中,若动点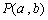 到两直线
到两直线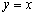 和
和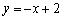 的距离之和为
的距离之和为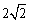 ,则
,则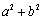 的最大值为 .
的最大值为 .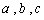 均为正数,证明:
均为正数,证明: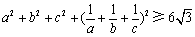 .
. 中,既与
中,既与 也与
也与 共面的棱的条数为
共面的棱的条数为 
 ,求满足
,求满足 且在圆
且在圆
 上的点
上的点 的坐标
的坐标 的前
的前 项和为
项和为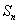 ,数列
,数列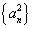 的前
的前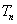 ,且
,且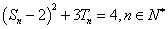 .
.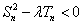 对
对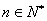 恒成立,求
恒成立,求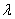 的最小值;
的最小值;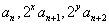 成等差数列,求正整数
成等差数列,求正整数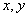 的值.
的值.