题目内容
对于函数f(x)=
的单调性表述正确的是( )
| 1-2x |
| x-1 |
| A、在(-∞,1)∪(1,+∞)上递增 |
| B、在(-∞,1)∪(1,+∞)上递减 |
| C、在(-∞,1),(1,+∞)上均递增 |
| D、在(-∞,1),(1,+∞)上均递减 |
考点:函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:化简后借助于反比例函数的单调性判断.
解答:
解:f(x)=
=-2-
,
则由反比例函数的单调性可知,
f(x)在(-∞,1),(1,+∞)上都是递增函数.
故选C.
| 1-2x |
| x-1 |
| 1 |
| x-1 |
则由反比例函数的单调性可知,
f(x)在(-∞,1),(1,+∞)上都是递增函数.
故选C.
点评:本题考查了函数单调性的判断,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
执行下面的框图,若输入的n是6,则输出p的值是( )


| A、120 | B、720 |
| C、1440 | D、5040 |
已知数列1,
,
,2,
,…则3
是它的( )
| 2 |
| 3 |
| 5 |
| 3 |
| A、第25项 | B、第26项 |
| C、第27项 | D、第28项 |
函数f(x)=lnx+x2+5的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |
斜率为1的直线l经过抛物线y2=2x的焦点,且与抛物线相交于A、B两点,则线段AB的长是( )
A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |
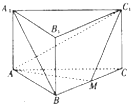 如图,已知三棱柱P-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱P-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC的中点.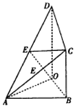 如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,
如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,