题目内容
4.函数f(x)=|2x•log${\;}_{\frac{1}{2}}$x|-1的零点个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由f(x)=0,转化为老公函数的交点,作出两个函数的图象,利用数形结合即可得到结论.
解答 解:∵f(x)=|2x•log${\;}_{\frac{1}{2}}$x|-1,
∴由f(x)=0得|$lo{g}_{\frac{1}{2}}x$|=2-x,作出y=|$lo{g}_{\frac{1}{2}}x$|,y=2-x的图象,
由图象可知两个图象的交点个数为2个,
故选:B.
点评 本题主要考查根的个数的判断,利用数形结合是解决本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
15. 执行如图所示的程序框图,则输出的结果为( )
执行如图所示的程序框图,则输出的结果为( )
 执行如图所示的程序框图,则输出的结果为( )
执行如图所示的程序框图,则输出的结果为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
19.已知i为虚数单位,复数z满足$\overline z(1+i)=i$,则z=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
9.已知点A(-1,2),B(2,3),直线l:kx-y-k+1=0与线段AB相交,则实数k的取值范围是( )
| A. | -$\frac{1}{2}$≤k≤2 | B. | k≤-$\frac{1}{2}$或k≥2 | C. | -2≤k≤$\frac{1}{2}$ | D. | k≤-2或k≥$\frac{1}{2}$ |
13.设α,β,γ表示平面,l表示直线,则下列命题中,错误的是( )
| A. | 如果α⊥β,那么α内一定存在直线平行于β | |
| B. | 如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ | |
| C. | 如果α不垂直于β,那么α内一定不存在直线垂直于β | |
| D. | 如果α⊥β,那么α内所有直线都垂直于β |
14.函数$f(x)=\frac{1}{x}$的导数是( )
| A. | $\frac{1}{x^2}$ | B. | $-\frac{1}{x^2}$ | C. | $\frac{1}{2x}$ | D. | $-\frac{1}{2x}$ |
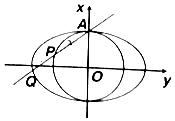 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=b2,过椭圆C的上顶点A的直线l:y=kx+b分别交圆O、椭圆C于不同的两点P、Q,设$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=b2,过椭圆C的上顶点A的直线l:y=kx+b分别交圆O、椭圆C于不同的两点P、Q,设$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.