题目内容
7.三棱锥A-BCD中,DA⊥AC,DB⊥BC,DA=AC,DB=BC,AB=$\frac{{\sqrt{2}}}{2}$CD,若三棱锥A-BCD的体积为$\frac{{2\sqrt{2}}}{3}$,则CD的长为( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 取CD的中点M,连接AM,BM,用CD表示出AM,BM,AB,证明CD⊥平面ABM,于是V=$\frac{1}{3}{S}_{△ABM}•CD$,列方程解出CD.
解答  解:取CD的中点M,连接AM,BM,
解:取CD的中点M,连接AM,BM,
∵DA⊥AC,DB⊥BC,DA=AC,DB=BC,
∴AM⊥CD,BM⊥CD,CM=DM,
∴CD⊥平面ABM,
∴V=$\frac{1}{3}{S}_{△ABM}•CD$.
设CD=x,则AM=BM=$\frac{x}{2}$,AB=$\frac{\sqrt{2}}{2}x$,
∴AM2+BM2=AB2,∴AM⊥BM,
∴S△ABM=$\frac{1}{2}×\frac{x}{2}×\frac{x}{2}$=$\frac{{x}^{2}}{8}$,
∴V=$\frac{1}{3}×\frac{{x}^{2}}{8}×x$=$\frac{{x}^{3}}{24}$=$\frac{2\sqrt{2}}{3}$,
∴x=2$\sqrt{2}$.
故选B.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
18.已知命题“?x∈R,ax2+4x+1>0”是假命题,则实数a的取值范围是( )
| A. | (4,+∞) | B. | (0,4] | C. | (-∞,4] | D. | [0.4) |
2.定义在(0,+∞)上的函数f(x)的导函数f′(x)满足$\sqrt{x}{f^'}(x)<\frac{1}{2}$,则下列不等式中,一定成立的是( )
| A. | f(9)-1<f(4)<f(1)+1 | B. | f(1)+1<f(4)<f(9)-1 | C. | f(5)+2<f(4)<f(1)-1 | D. | f(1)-1<f(4)<f(5)+2 |
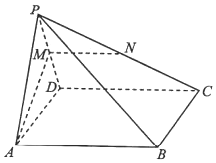 如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证: