题目内容
8.已知p:方程x2+mx+1=0有两个不等的正实根;q:方程4x2+4(m-2)x+1=0无实数根.若p∨q为真,p∧q为假,求实数m的取值范围.分析 若p∨q为真,p∧q为假,则p真q假或p假q真,分类讨论,可得满足条件的实数m的取值范围.
解答 解:若命题p为真:
则$\left\{\begin{array}{l}△>0\\{x_1}+{x_2}>0\\{x_1}{x_2}>0\end{array}\right.$,
即$\left\{\begin{array}{l}{m^2}-4>0\\-m>0\\ 1>0\end{array}\right.$,
⇒m<-2
若命题q为真,
则△<0,即16(m-2)2-16<0
⇒1<m<3
∵p∨q为真,p∧q为假
∴p真q假或p假q真
当p真q假时,$\left\{\begin{array}{l}m<-2\\ m≤1或m≥3\end{array}\right.$⇒m<-2
当p假q真时,$\left\{\begin{array}{l}m≥-2\\ 1<m<3\end{array}\right.$⇒1<m<3
综上所述m<-2或1<m<3
点评 本题以命题的真假判断与应用为载体,考查了复合命题,方程根与关系等知识点,难度中档.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
19.下列命题中,真命题的是( )
| A. | 存在x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | B. | 任意x∈(3,+∞),x2>3x-1 | ||
| C. | 存在x∈R,x2+x=-1 | D. | 任意x∈($\frac{π}{2}$,π),tanx>sinx |
13.已知不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≥-1\\ y≥0\end{array}\right.$所表示的平面区域为D.若目标函数z=ax-y-2在区域D上的最大值为2,则实数a的值为( )
| A. | -2 | B. | 4 | C. | -2或4 | D. | -4或4 |
20.复数z=$\frac{1+2i}{1+i}$(i为虚数单位)在复平面内对应点的坐标是( )
| A. | ($\frac{3}{2}$,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{3}{2}$,$\frac{1}{2}$) |
18.设a,b是不同的直线,α、β是不同的平面.下列命题中正确的是( )
| A. | 若a⊥α,b∥β,a⊥b,则α⊥β | B. | 若a⊥α,b∥β,a∥b,则α∥β | ||
| C. | 若a⊥α,a∥β,则α⊥β | D. | 若a∥β,b∥β,则α∥b |
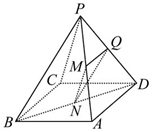 如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,
如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,