题目内容
3．
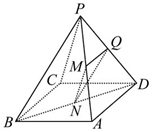如图，已知四棱锥P-ABCD中，底面ABCD为平行四边形，点M，N，Q分别是PA，BD，PD的中点上，（1）求证：MN∥PC；
（2）求证：平面MNQ∥平面PBC．
分析 （1）利用底面ABCD为平行四边形，点M，N，Q分别是PA，BD，PD的中点上，连接AC，可得MN是三角形ACP的中位线，可得MN∥PC．
（2）面面平行转化为线线平行，证明一个平面内的两天直线分别平行另一个平面，并且这两条直线要相交，求利用三角形ADP的中位线MQ∥PB，MN∥PC，可得平面MNQ∥平面PBC．
解答 解：（1）由题意：P-ABCD是四棱锥，底面ABCD为平行四边形，点M，N，Q分别是PA，BD，PD的中点上，连接AC，∴N是AC的中点．
∴MN是三角形ACP的中位线，
∴MN∥PC．
（2）由（1）可得MN∥PC．
∵M，Q分别在PA，PD的中点上，
∴MQ是三角形ADP的中位线，
∴MQ∥PB．
由MQ∥PB，MN∥PC，PB?平面PBC，PC?平面PBC，PB∩PC=P，
同理MQ?平面MNQ，MN?平面MNQ，MQ∩MN=M．
∴平面MNQ∥平面PBC．
点评 本题考察了线线平行和面面平行的证明，利用了三角形的中位线这性质．比较基础题．
练习册系列答案
相关题目
13．对于二次函数y=-$\frac{1}{4}$x2+x-4，下列说法正确的是（ ）
| A． | 当x＞0时，y随x的增大而增大 | B． | 当x=2时，y有最大值-3 | ||
| C． | 图象的顶点坐标为（-2，-7） | D． | 图象与x轴有两个交点 |
14．设集合 A={x|x=$\frac{k}{4}$+$\frac{1}{2}$，k∈Z}，B={x|x=$\frac{k}{2}$+$\frac{1}{4}$，k∈Z}，则集合 A 与 B 的关系是（ ）
| A． | A?B | B． | B?A | ||
| C． | A=B | D． | A 与 B 关系不确定 |
11．设全集∪={a，b，c，d}，集合M={ a，c，d }，N={b，d}，则（∁UM）∩N等于（ ）
| A． | {b} | B． | {d} | C． | {a，c} | D． | {b，d} |