题目内容
已知圆C1：（x-1）2+（y-2）2=9，C2：（x+3）2+（y-1）2=1，则两圆的外公切线段长等于 ．
考点：圆的切线方程
专题：直线与圆
分析：先求出两个圆的圆心和半径，可得两个圆相离，作辅助线，构造直角三角形，利用勾股定理求得公切线的长度．
解答：
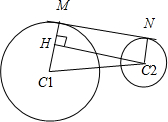解：由题意可得，圆心C1（1，2），半径为3；
圆心C2（-3，1），半径为1，由于圆心距|C1C2|=
＞3+1，
故两个圆相离．
设两圆的公切线的切点分别为M、N，练接C1M、C2N、C1C2，
作C2H⊥C1M，H为垂足，则|C2H|即为所求．
直角三角形C1C2H中，由勾股定理可得|C2H|=
=
=
，
故答案为：
．
解：由题意可得，圆心C1（1，2），半径为3；圆心C2（-3，1），半径为1，由于圆心距|C1C2|=
| 17 |
故两个圆相离．
设两圆的公切线的切点分别为M、N，练接C1M、C2N、C1C2，
作C2H⊥C1M，H为垂足，则|C2H|即为所求．
直角三角形C1C2H中，由勾股定理可得|C2H|=
| (C1C2)2-(C1H)2 |
=
| 17-(3-1)2 |
| 13 |
故答案为：
| 13 |
点评：本题主要考查两个圆的位置关系、两圆的公切线的性质，体现了数形结合的数学思想，属于中档题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
设全集为U=R，集合A=（-∞，-3]∪[6，+∞），B={x|-2＜x＜8}．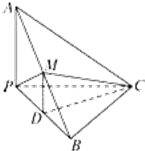
如图，已知三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．