题目内容
3.某学校星期一至星期五每天上午共安排五节课,每节课的时间为40分钟,第一节课上课时间为7:50~8:30,课间休息10分钟,某同学请假后返校,若他在8:50~9:30之间随机到达教室,则他听第二节课的时间不少于20分钟的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 他在8:50~9:30之间随机到达教室,区间长度为50,他听第二节课的时间不少于20分钟,则他在8:50~9:00之间随机到达教室,区间长度为10,即可求出概率.
解答 解:他在8:50~9:30之间随机到达教室,区间长度为50,他听第二节课的时间不少于20分钟,则他在8:50~9:00之间随机到达教室,区间长度为10,
∴他在8:50~9:30之间随机到达教室,则他听第二节课的时间不少于20分钟的概率是$\frac{1}{5}$,
故选:A.
点评 本题主要考查几何概型中的长度类型,解决的关键是找到问题的分界点,分清是长度,面积,还是体积类型,再应用概率公式求解.

练习册系列答案
相关题目
13.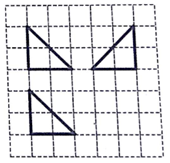 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球的表面积为( )| A. | $4\sqrt{3}π$ | B. | 12π | C. | 48π | D. | $32\sqrt{3}π$ |
18.已知实数x,y满足$\left\{\begin{array}{l}{x-y+6≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$若目标函数Z=ax+y的最大值为3a+9,最小值为3a-3,则实数a的取值范围是( )
| A. | {a|-1≤a≤1} | B. | {a|a≤-1} | C. | {a|a≤-1或a≥1} | D. | {a|a≥1} |
8.等差数列{an}中,a7=4,a8=1,则a10=( )
| A. | -5 | B. | -2 | C. | 7 | D. | 10 |
12.设实数x,y满足$\left\{\begin{array}{l}x+y-6≥0\\ x+2y-14≤0\\ 2x+y-10≤0\end{array}\right.$,则2xy的最大值为( )
| A. | 25 | B. | 49 | C. | 12 | D. | 24 |
13.已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
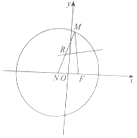 已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.
已知点N(-1,0),F(1,0)为平面直角坐标系内两定点,点M是以N为圆心,4为半径的圆上任意一点,线段MF的垂直平分线交于MN于点R.