题目内容
15.将5幅不同的冬奥会宣传作品排成前后两排展出,每排至少2幅,其中A,B两幅作品必须排在前排,那么不同的排法共有48种.分析 根据题意,分2种情况讨论:①、前排2幅,后排3幅,②、前排3幅,后排2幅,每种情况下依次分析前排和后排的排法数目,即可得每种下的排法数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、前排2幅,后排3幅,则前排的必须是A,B,考虑其顺序,有A22=2种情况,
剩下的三幅放在后排,有A33=6种情况,
则此时有2×6=12种不同的排法,
②、前排3幅,后排2幅,
需要先在剩下3幅中,选出1幅,与A、B一起放在前排,有C31A33=18种情况,
剩下的2幅放在后排,考虑其顺序,有A22=2种情况,
则此时有18×2=36种不同的排法,
则不同的排法共有12+36=48种;
故答案为:48.
点评 本题考查排列、组合的综合运用,注意依据题意的要求,进行分类讨论.

练习册系列答案
相关题目
3.某学校星期一至星期五每天上午共安排五节课,每节课的时间为40分钟,第一节课上课时间为7:50~8:30,课间休息10分钟,某同学请假后返校,若他在8:50~9:30之间随机到达教室,则他听第二节课的时间不少于20分钟的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
10.如图是一个算法的程序框图,如果输入i=0,S=0,那么输出的结果为( )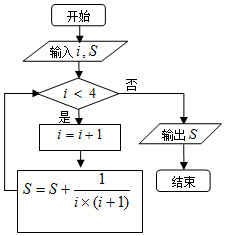

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
7.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领到的钱数不少于其他任何人)的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |
4.为了得到函数y=4sinxcosx,x∈R的图象,只要把函数y=sin2x-$\sqrt{3}$cos2x,x∈R图象上所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
5.在平面直角坐标系xOy中,双曲线C的一个焦点为F(2,0),一条渐近线的倾斜角为60°,则C的标准方程为( )
| A. | $\frac{x^2}{3}-{y^2}=1$ | B. | $\frac{y^2}{3}-{x^2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | ${y^2}-\frac{x^2}{3}=1$ |
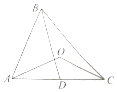 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$. 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.