题目内容
14.己知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点O是坐标原点,点P是椭圆C上任意一点,且点M满足$\overrightarrow{OM}=λ\overrightarrow{OP}$(λ>1,λ是常数).当点P在椭圆C上运动时,点M形成的曲线为Cλ.(I)求曲线Cλ的轨迹方程;
(II)直线l是椭圆C在点P处的切线,与曲线Cλ的交点为A,B两点,探究△OAB的面积是否为定值.若是,求△OAB的面积,若不是,请说明理由.
分析 (Ⅰ)设点M的坐标为(x,y),对应的点P的坐标为($\frac{x}{λ}$,$\frac{y}{λ}$),由点P在椭圆C上得曲线Cλ的轨迹方程为$\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1,(λ>1)$.
(Ⅱ)由△=0,得过点A(x1,y1)的切线方程为$\frac{{x}_{1}x}{4}+{y}_{1}y=1$,设切点A(x2,y2),B(x3,y3)
联立$\left\{\begin{array}{l}{\frac{{x}_{1}}{4}x+{y}_{1}y=1}\\{\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1}\end{array}\right.$,结合$\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2}=1$得4x2-8x1x+16-16${{y}_{1}}^{2}{λ}^{2}$=0,可得|AB|=$\sqrt{1+(-\frac{{x}_{1}}{4{y}_{1}})^{2}}$×|x3-x4|,原点O到直线AB的距离d=$\frac{1}{\sqrt{\frac{{{x}_{1}}^{2}}{16}+{{y}_{1}}^{2}}}=\frac{4}{\sqrt{{{x}_{1}}^{2}+16{{y}_{1}}^{2}}}$,△OAB的面积s=$\frac{1}{2}×$|AB|×d=$\frac{1}{2}×$$\sqrt{16{{y}_{1}}^{2}+{{x}_{1}}^{2}}•\sqrt{{λ}^{2}-1}$×$\frac{4}{\sqrt{{{x}_{1}}^{2}+16{{y}_{1}}^{2}}}$=2$\sqrt{{λ}^{2}-1}$(定值)
解答 解:(Ⅰ)设点M的坐标为(x,y),对应的点P的坐标为($\frac{x}{λ}$,$\frac{y}{λ}$)
由于点P在椭圆C上,得,$\frac{(\frac{x}{λ})^{2}}{4}+(\frac{y}{λ})^{2}=1$
即曲线Cλ的轨迹是椭圆,标准方程为$\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1,(λ>1)$.
(Ⅱ)①当过点P(x1,y1)切线的斜率存在时,
设该切线的方程为y-y1=k(x-x1),即y=kx+(y1-kx1)
联立y=kx+(y1-kx1)、椭圆C:$\frac{x^2}{4}+{y^2}$=1
得(${k}^{2}+\frac{1}{4}$)x2+2k(y1-kx1)x+[(y1-kx1)2-1]=0
,由△=0,得1+4k2=[(y1-kx1)2,的k=-$\frac{{x}_{1}}{4{y}_{1}}$.
此时过点A(x1,y1)的切线方程为$\frac{{x}_{1}x}{4}+{y}_{1}y=1$
过点P切线的斜率不存在时,切点为(±2,0),方程为x=±2,
符合方程为$\frac{{x}_{1}x}{4}+{y}_{1}y=1$.
∴过点P的切线方程为$\frac{{x}_{1}x}{4}+{y}_{1}y=1$.
设A(x2,y2),B(x3,y3)
联立$\left\{\begin{array}{l}{\frac{{x}_{1}}{4}x+{y}_{1}y=1}\\{\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1}\end{array}\right.$,结合$\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2}=1$得4x2-8x1x+16-16${{y}_{1}}^{2}{λ}^{2}$=0
${x}_{3}+{x}_{4}=2{x}_{1},{x}_{3}{x}_{4}=4-4{{y}_{1}}^{2}{λ}^{2}$
∴|AB|=$\sqrt{1+(-\frac{{x}_{1}}{4{y}_{1}})^{2}}$×|x3-x4|=$\sqrt{16{{y}_{1}}^{2}+{{x}_{1}}^{2}}•\sqrt{{λ}^{2}-1}$.
原点O到直线AB的距离d=$\frac{1}{\sqrt{\frac{{{x}_{1}}^{2}}{16}+{{y}_{1}}^{2}}}=\frac{4}{\sqrt{{{x}_{1}}^{2}+16{{y}_{1}}^{2}}}$
∴△OAB的面积s=$\frac{1}{2}×$|AB|×d=$\frac{1}{2}×$$\sqrt{16{{y}_{1}}^{2}+{{x}_{1}}^{2}}•\sqrt{{λ}^{2}-1}$×$\frac{4}{\sqrt{{{x}_{1}}^{2}+16{{y}_{1}}^{2}}}$=2$\sqrt{{λ}^{2}-1}$(定值)
故△OAB的面积是定值2$\sqrt{{λ}^{2}-1}$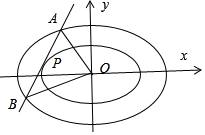
点评 本题考查了椭圆的方程与性质,椭圆的切线方程及用弦长、距离表示三角形面积,考查了方程思想、转化思想,属于难题.

| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
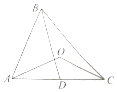 如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.
如图,在锐角△ABC中,D为AC边的中点,且BC=$\sqrt{2}BD=2\sqrt{2}$,O为△ABC外接圆的圆心,且cos∠AOC=-$\frac{3}{4}$.