题目内容
已知公差大于零的等差数列{an},各项均为正数的等比数列{bn},满足a1=1,b1=2,a4=b2,a8=b3 求数列{an}和{bn}的通项公式.
考点:等比数列的通项公式,等差数列的通项公式
专题:等差数列与等比数列
分析:设数列{an}的公差为d(d>0),数列{bn}的公比为q,由等比中项的性质,求得得公差和公比,代入等差数列和等比数列的通项公式得答案;
解答:
解:设数列{an}的公差为d(d>0),数列{bn}的公比为q,
∵a1=1,b1=2,a4=b2=a1+3d=1+3d,a8=b3=a1+7d=1+7d,
∴b22=b1•b3,
∴(1+3d)2=1×(1+7d),
解得d=
,或d=0(舍去),
∴a4=b2=a1+3d=1+3d=1+
=
,
∴q=
=
,
∴an=1+
(n-1)=
(n+2),bn=(
)n-1,
∵a1=1,b1=2,a4=b2=a1+3d=1+3d,a8=b3=a1+7d=1+7d,
∴b22=b1•b3,
∴(1+3d)2=1×(1+7d),
解得d=
| 1 |
| 9 |
∴a4=b2=a1+3d=1+3d=1+
| 1 |
| 3 |
| 4 |
| 3 |
∴q=
| b2 |
| b1 |
| 4 |
| 3 |
∴an=1+
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查了等差数列和等比数列的通项公式,属于基础题

练习册系列答案
相关题目
已知A={x|y=x2-1},B={y|y=x2-1},则A∩B( )
| A、∅ | B、A | C、B | D、R |

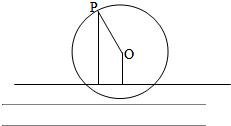 如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(-
如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(-