��Ŀ����
11��������ʵ��x0����ʵ����x��ʹ�ú���f��x������f��x0+��x��=f��x0��+4k��x��������k��1������ƺ���f��x��Ϊ��k�����������������ĸ�������${f_{\;}}��x��=\sqrt{x}$
��${f_{\;}}��x��={x^2}-2xx��[0��3]$
��f��x��=4sinx
��${f_{\;}}��x��={e^x}-lnx$
����Ϊ��k�����������Т٢ܣ����������ȷ���۵ķ��ţ���
���� �������¶��壬ͨ��ѡȡʵ��x0����ʵ����x���жϺ����Ƿ������¶��弴�ɣ����ж��¶��岻�����������Ƴ�������ۢ����ñ���ʽ�ļ������壬ͨ�������ĵ�����⼴�ɣ�
��� �⣺���ڢ�${f_{\;}}��x��=\sqrt{x}$����ʵ��x0=0����ʵ����x=$\frac{1}{16{k}^{2}}$��
�ɵã�f��x0+��x��=$\sqrt{��x}$=$\frac{1}{4k}$��
f��x0��+4k��x=4k��$\frac{1}{16{k}^{2}}$=$\frac{1}{4k}$��
����f��x������f��x0+��x��=f��x0��+4k��x��������k��1����
����f��x����k����������
���ڢ�${f_{\;}}��x��={x^2}-2xx��[0��3]$
f��x0+��x��=��x0+��x��2-2��x0+��x��=x02+2x0��x+��x2-2x0-2��x��
f��x0��+4k��x=x02-2x0+4k��x��
������f��x0+��x��=f��x0��+4k��x��
����2x0��x+��x2-2��x=4k��x��
����2x0+��x-2=4k����x��[0��3]��x0+��x��[0��3]��x0+��x-2��[-2��1]��x0��3��
��2x0+��x-2��4��
��ں���f��x�����ǡ�k����������
���ڣ���f��x��=4sinx��������f��x������f��x0+��x��=f��x0��+4k��x��
�������֪�������������⣬
����4k=$\frac{f��{x}_{0}+��x��-f��{x}_{0}��}{��x}$�����������������ߵ�б�ʱ�����ڡ�4��б�ʣ�
f�䣨x��=4cosx��
��f�䣨��x��=4cos��x��4��
��۰��������⣮
���ڢܣ�${f_{\;}}��x��={e^x}-lnx$���������������⣬
����4k=$\frac{f��{x}_{0}+��x��-f��{x}_{0}��}{��x}$�����������������ߵ�б�ʱ�����ڡ�4��б�ʣ�
f�䣨x��=ex-$\frac{1}{x}$��f�䣨��x��=${e}^{��x}-\frac{1}{��x}$��R��
���Ԣ��������⣬
�ʴ�Ϊ���٢ܣ�
���� ���⿼���¶����Ӧ�ã���ֵ���Լ�ֱ�ӷ��������ĵ������ۺ�Ӧ�ã��������������������������ѶȱȽϴ�

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�| A�� | 66 | B�� | 78 | C�� | 105 | D�� | 120 |
| A�� | 6 | B�� | -6 | C�� | $2\sqrt{3}$ | D�� | $-2\sqrt{3}$ |
| A�� | {x|x$��-\sqrt{2}$} | B�� | {x|-$\sqrt{2}$��x��-1} | C�� | {x|-$\sqrt{2}��x��\sqrt{2}$} | D�� | {x|-1$��x��\sqrt{2}$} |
| A�� | ��1��3�� | B�� | ��1��2] | C�� | $��\frac{1}{2}��\frac{7}{2}��$ | D�� | ���Ͼ�����ȷ |
| A�� | ������ģ������ʵ�� | |
| B�� | �������븴ƽ��������������ɵļ���һһ��Ӧ | |
| C�� | ����븴��z��Ӧ�ĵ��ڵ�һ���ޣ�����ø�����Ӧ���������յ�Ҳһ�����ڵ�һ���� | |
| D�� | ��ȵ�������Ӧ����ȵĸ��� |
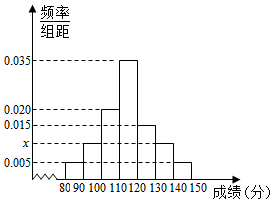 40������ѧ��ij����ѧ���Գɼ�����λ���֣���Ƶ�ʷֲ�ֱ��ͼ��ͼ��
40������ѧ��ij����ѧ���Գɼ�����λ���֣���Ƶ�ʷֲ�ֱ��ͼ��ͼ��