题目内容
17．（1+x）n展开式中有连续四项的前三项二项式系数成等差数列，后两项二项式系数相同，则这个展开式共有（ ）| A． | 5项 | B． | 6项 | C． | 7项 | D． | 8项 |
分析 由条件利用等差数列的定义性质，组合数的计算公式，求得r的值，可得n的值，从而根据二项式定理得出结论．
解答 解：设（1+x）n展开式中有连续四项分别为第r+1、r+2、r+3、r+4项，
根据这四项的前三项二项式系数成等差数列，后两项二项式系数相同，
可得${C}_{n}^{r}$+${C}_{n}^{r+2}$=2${C}_{n}^{r+1}$ ①，且${C}_{n}^{r+2}$=${C}_{n}^{r+3}$ ②．
由②可得 n=2r+5，代入①可得${C}_{2r+5}^{r}$+${C}_{2r+5}^{r+2}$=2${C}_{2r+5}^{r+1}$，
即$\frac{（2r+5）!}{r!•（r+5）!}$+$\frac{（2r+5）!}{（r+2）!•（r+3）!}$=2$\frac{（2r+5）!}{（r+1）!•（r+4）!}$，
求得r=1，∴n=7，故这个展开式共有8项，
故选：D．
点评 本题主要考查二项式定理的应用，等差数列的定义性质，组合数的计算公式，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知在△ABC中，角A，B，C所对的边分别为a，b，c．若∠ABC=$\frac{π}{3}$，b=$\sqrt{7}$，c=2，D为BC的中点．
5．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上一点与其左顶点、右焦点构成以右焦点为直角顶点的等腰三角形，则此双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 2$+\sqrt{2}$ |
2．设单位向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的夹角为$\frac{2π}{3}$，$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$，则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为（ ）
| A． | -$\frac{3\sqrt{3}}{2}$ | B． | -$\frac{2\sqrt{3}}{2}$ | C． | $\frac{2\sqrt{3}}{2}$ | D． | $\frac{3\sqrt{3}}{2}$ |
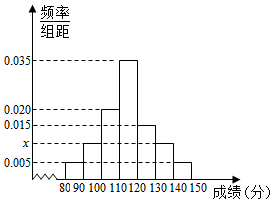40名高三学生某次数学考试成绩（单位：分）的频率分布直方图如图：