题目内容
9.函数y=3sin($\frac{π}{4}$-3x)+$\sqrt{3}$cos($\frac{π}{4}$-3x)的最小正周期是( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | 8 | D. | 4 |
分析 利用辅助角公式化简函数的解析式,再利用正弦函数的周期性求得函数的最小正周期.
解答 解:∵函数y=3sin($\frac{π}{4}$-3x)+$\sqrt{3}$cos($\frac{π}{4}$-3x)
=2$\sqrt{3}$[$\frac{\sqrt{3}}{2}$sin($\frac{π}{4}$-3x)+$\frac{1}{2}$cos($\frac{π}{4}$-3x)]
=2$\sqrt{3}$sin[($\frac{π}{4}$-3x)+$\frac{π}{6}$]=2$\sqrt{3}$sin($\frac{5π}{12}$-3x)=-2$\sqrt{3}$sin(3x-$\frac{5π}{12}$),
∴该函数的最小正周期为$\frac{2π}{3}$,
故选:A.
点评 本题主要考查辅助角公式的应用,正弦函数的周期性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.观察下列各式:55=3125,56=15625,57=78125,…,则52016的末四位数字为( )
| A. | 3125 | B. | 5625 | C. | 0625 | D. | 8125 |
4.已知cosθ=$\frac{1}{3}$,θ∈(0,π),则cos($\frac{π}{2}$+2θ)的值为( )
| A. | $\frac{4\sqrt{2}}{9}$ | B. | -$\frac{7}{9}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
19.设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)-f′(x)<1,f(0)=2016,则不等式f(x)>2015ex+1的解集为( )
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2015,+∞) | D. | (-∞,0)∪(2015,+∞) |
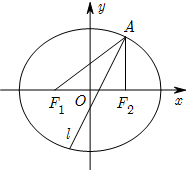 已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,焦距与长轴长的比为$\frac{1}{2}$.
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,焦距与长轴长的比为$\frac{1}{2}$.