题目内容
9.在等比数列{an}中,已知a3=1,a5=3,则$\frac{{a}_{2011}+{a}_{2012}}{{a}_{2009}+{a}_{2010}}$=3.分析 根据题意,由所给的a3=1和a5=3可得$\frac{{a}_{5}}{{a}_{3}}$=q2=3,而$\frac{{a}_{2011}+{a}_{2012}}{{a}_{2009}+{a}_{2010}}$=$\frac{{a}_{2009}•{q}^{2}+{a}_{2010}•{q}^{2}}{{a}_{2009}+{a}_{2010}}$,将q2=3代入可得答案.
解答 解:根据题意,等比数列{an}中,已知a3=1,a5=3,
则$\frac{{a}_{5}}{{a}_{3}}$=q2=3,
故$\frac{{a}_{2011}+{a}_{2012}}{{a}_{2009}+{a}_{2010}}$=$\frac{{a}_{2009}•{q}^{2}+{a}_{2010}•{q}^{2}}{{a}_{2009}+{a}_{2010}}$=q2=3,
故答案为:3.
点评 本题考查等比数列的通项公式及其运用,注意分析分子分母中项与项之间的关系.

练习册系列答案
相关题目
19.在△ABC中,若AB=4,BC=5,B=60°,则AC=( )
| A. | $\sqrt{21}$ | B. | $\sqrt{31}$ | C. | $\sqrt{51}$ | D. | $\sqrt{61}$ |
4.若全集U=R,集合A={x|0<x<2},B={x|x-1>0},则A∩∁UB=( )
| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
11.已知集合$A=\{1,2014,\frac{1}{2014}\}$,B={y|y=log2014x,x∈A},则A∩B=( )
| A. | $\{\frac{1}{2014}\}$ | B. | {2014} | C. | {1} | D. | ∅ |
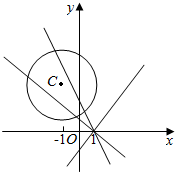 已知圆C的方程为(x+1)2+(y-3)2=4,过点(1,0)的直线l的斜率为k,设圆C上到l的距离为l的点的个数z,求z关于k的函数关系式.
已知圆C的方程为(x+1)2+(y-3)2=4,过点(1,0)的直线l的斜率为k,设圆C上到l的距离为l的点的个数z,求z关于k的函数关系式.