题目内容
19.在数列{an}(n∈N*)中,设a1=a2=1,a3=2.若数列{$\frac{{a}_{n+1}}{{a}_{n}}$}是等差数列,则a6=120.分析 由数列{$\frac{{a}_{n+1}}{{a}_{n}}$}是等差数列,结合已知求得$\frac{{a}_{n+1}}{{a}_{n}}=n$,然后利用累积法求得a6.
解答 解:∵数列{$\frac{{a}_{n+1}}{{a}_{n}}$}是等差数列,
∴公差d=$\frac{{a}_{3}}{{a}_{2}}-\frac{{a}_{2}}{{a}_{1}}=\frac{2}{1}-\frac{1}{1}=1$.
则$\frac{{a}_{n+1}}{{a}_{n}}=1+1×(n-1)=n$.
则$\frac{{a}_{2}}{{a}_{1}}=1,\frac{{a}_{3}}{{a}_{2}}=2,\frac{{a}_{4}}{{a}_{3}}=3$,…$\frac{{a}_{6}}{{a}_{5}}=5$.
累积得:$\frac{{a}_{6}}{{a}_{1}}=1×2×3×4×5$,
∴a6=120.
故答案为:120.
点评 本题考查等差数列的通项公式,考查了累加法,是基础的计算题.

练习册系列答案
相关题目
10.已知双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点分别为F1,F2,若E上存在点P使△F1F2P为等腰三角形,且其顶角为$\frac{2π}{3}$,则$\frac{a^2}{b^2}$的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
7.已知平面向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(y,1).若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x,y一定满足( )
| A. | xy-1=0 | B. | xy+1=0 | C. | x-y=0 | D. | x+y=0 |
14.在空间中,设l,m为两条不同直线,α,β为两个不同的平面,则下列命题正确的是( )
| A. | 若l?α,m不平行于l,则m不平行于α | |
| B. | 若l?α,m?β,且α,β不平行,则l,m不平行 | |
| C. | 若l?α,m不垂直于l,则m不垂直于α | |
| D. | 若l?α,m?β,l不垂直于m,则α,β不垂直 |
8.已知x>3,则$x+\frac{4}{x-3}$的最小值为( )
| A. | 2 | B. | 4 | C. | 5 | D. | 7 |

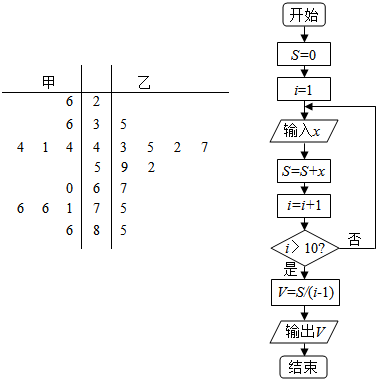 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.