题目内容

8．已知x＞3，则$x+\frac{4}{x-3}$的最小值为（　　）
A．2B．4C．5D．7

分析 利用基本不等式直接求解表达式的最小值即可．

解答 解：x＞3，则$x+\frac{4}{x-3}$=$x-3+\frac{4}{x-3}+3$≥$2\sqrt{（x-3）•\frac{4}{x-3}}+3$=7．
当且仅当x=5时等号成立．
故选：D．

点评 本题考查基本不等式在最值中的应用，考查转化思想以及计算能力，注意表达式的变形是解题的关键．

练习册系列答案
相关题目
18．形如$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|$的符号叫二阶行列式，现规定$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|$=a11•a22-a21•a12，如果f（θ）=$|\begin{array}{l}{sinθ}&{cosθ}\\{cos\frac{2π}{3}}&{sin\frac{7π}{3}}\end{array}|$=$|\begin{array}{l}{\sqrt{2}}&{-2\sqrt{2}}\\{1}&{-\frac{3}{2}}\end{array}|$θ∈（0，π），则θ=$\frac{π}{12}$或$\frac{7π}{12}$．
19．在数列{an}（n∈N*）中，设a1=a2=1，a3=2．若数列{$\frac{{a}_{n+1}}{{a}_{n}}$}是等差数列，则a6=120．
16．若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域被直线y=kx+2分为面积相等的两部分，则k的值为$\frac{1}{2}$；若该平面区域存在点（x0，y0）使x0+ay0+2≤0成立，则实数a的取值范围是a≤-1．
3．阅读如图所示的程序框图，运行相应的程序，输出的结果为（　　）
A．2B．4C．6D．8
13．从自然数1，2，3，4，5中，任意取出两个数组成两位的自然数，则在两位自然数中取出的数恰好能被3整除的概率为（　　）
A．$\frac{2}{5}$B．$\frac{1}{5}$C．$\frac{3}{10}$D．$\frac{1}{2}$
20．在平面直角坐标系xOy中，已知圆C：（x-2）2+（y+1）2=5，过点P（5，0）且斜率为k的直线l与圆C相交于不同的两点A，B．
（Ⅰ）求k的取值范围；
（Ⅱ）若弦长|AB|=4，求直线l的方程．
17．设全集U=C，A={z||z-1|=1-|z|，z∈C}，B={z||z|＜1，z∈C}，若z∈A∩（∁UB），求复数z在复平面内对应点的轨迹．
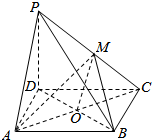18．如图，已知P为平行四边形ABCD所在平面外一点，M是线段PC的中点．
（1）求证：向量$\overrightarrow{PA}$，$\overrightarrow{MB}$，$\overrightarrow{MD}$共面；
（2）求证：向量$\overrightarrow{MA}$，$\overrightarrow{MB}$，$\overrightarrow{MC}$不共面；
（3）若向量$\overrightarrow{PD}$=x$\overrightarrow{MA}$+y$\overrightarrow{MB}$+z$\overrightarrow{MC}$，求x，y，z的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网