题目内容
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$-$\overrightarrow{a}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值为5.分析 由向量的共线的性质可得|$\overrightarrow{b}$|的最大值为2+1=3,由|$\overrightarrow{b}$-$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=t,两边平方可得8+2$\overrightarrow{b}$2=1+t2,可得最大值.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$-$\overrightarrow{a}$|=1,
可得|$\overrightarrow{b}$|的最大值为2+1=3,
由|$\overrightarrow{b}$-$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=t,
平方可得,|$\overrightarrow{b}$-$\overrightarrow{a}$|2+|$\overrightarrow{a}$+$\overrightarrow{b}$|2=t2+1,
即有2$\overrightarrow{a}$2+2$\overrightarrow{b}$2=1+t2,
即8+2$\overrightarrow{b}$2=1+t2,
可得t2的最大值为8+2×9-1=25,
即有|$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值为5.
故答案为:5.
点评 本题考查向量的模的最值的求法,注意运用向量共线和三角形三边的关系,考查向量的数量积的性质:向量的平方即为模的平方,属于中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案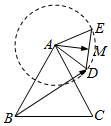 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
| A. | 3 | B. | -3 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | x1x2<1 | B. | x1x2>x1+x2 | C. | x1x2<x1+x2 | D. | x1x2=x1+x2 |
