题目内容

若θ∈R，则方程
.
2sin2θ1
11
.
=0的解为
 
．
考点：二阶矩阵,二倍角的正弦
专题：矩阵和变换
分析：由已知条件得sin2θ=
1
2
，由此能求出结果．
解答： 解：∵θ∈R，
方程
.
2sin2θ1
11
.
=2sin2θ-1=0，
∴sin2θ=
1
2
，
∴2θ=2kπ+
π
6
或2θ=2kπ+
5π
6
，k∈Z，
∴θ=kπ+
π
12
或θ=kπ+
5π
12
，k∈Z．
故答案为：θ=kπ+
π
12
或θ=kπ+
5π
12
，k∈Z．
点评：本题考查方程的解法，是基础题，解题时要注意二阶矩阵、三角函数知识点的合理运用．
练习册系列答案
相关题目
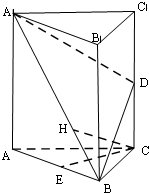如图，在三棱柱ABC-A1B1C1中，△ABC是边长为2的等边三角形，AA1⊥平面ABC，D，E分别是CC1，AB的中点．
（1）求证：CE∥平面A1BD；
（2）若H为A1B上的动点，CH与平面A1AB所成的最大角的正切值为
15
2
，求侧棱AA1的长．
已知曲线C：x2+y2=1，对它先作矩阵A=
10
02
对应的变换，再作矩阵B=
0b
10
对应的变换，得到曲线C：
x2
4
+y2=1．则实数b=
 
．
数列{an}前n项和Sn=n2+n+1，则an=
 
．
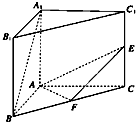设在直三棱柱ABC-A1B1C1中，AB=AC=AA1=2，∠BAC=90°，E，F依次为C1C，BC的中点．则异面直线A1B、EF所成角θ的大小
 
（用反三角函数值表示）．
若a=
6
-
2
，b=
3
-1，则a，b的大小关系为
 
．
小李晨练所花时间（单位：分钟）的样本数据分别为x，y，30，29，31；已知这组数据的平均数为30，方差为2，则|x-y|的值为
 
．
已知
2 1
3 2
A
2 2
5 3
=
2 4
1 3
，则A=
 
．
正四棱柱ABCD-A1B1C1D1中，AA1=3AB，则异面直线A1B与AD1所成角的余弦值为（　　）
A、
1
3
B、
5
10
C、
9
10
D、
4
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网