题目内容
8.如图,在由5个边长为1,一个顶角为60°的菱形组成的图形中,$\overrightarrow{AB}$•$\overrightarrow{CD}$=-4.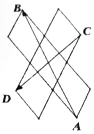
分析 建立坐标系,得出两向量的坐标,从而计算出数量积.
解答 解:以中间菱形的对角线为坐标轴建立如图所示的坐标系:
则A($\frac{1}{2}$,-$\sqrt{3}$),B(-$\frac{1}{2}$,$\sqrt{3}$),C(1,$\frac{\sqrt{3}}{2}$),D(-1,-$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AB}$=(-1,2$\sqrt{3}$),$\overrightarrow{CD}$=(-2,-$\sqrt{3}$),
∴$\overrightarrow{AB}•\overrightarrow{CD}$=2-6=-4.
故答案为:-4.
点评 本题考查了平面向量的数量积运算,建立坐标系可是计算简便,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
16.对于两个不重合的平面α与β,给定下列条件,其中可以判定α与β平行的条件是( )
| A. | α内有不共线的三点到β的距离相等; | |
| B. | a内存在直线平行于平面β | |
| C. | 存在平面γ,使得α⊥γ,β⊥γ | |
| D. | 存在异面直线l,m使得l∥α,l∥β,m∥α,m∥β |
13.已知集合A={x|x2+x-6<0},B={-2,-1,0,1,2},那么A∩B=( )
| A. | {-2,-1,0,1} | B. | {-2,-1,1} | C. | {-1,1,2} | D. | {-1,0,1,2} |
17.已知集合A={-2,-1,0,1,2,3},B={y|y=|x|-3,x∈A},则A∩B=( )
| A. | {-3,-2,-1,0} | B. | {-1,0,1,2} | C. | {-2,-1,0} | D. | {-1,0,1} |
18.已知全集U=R,集合A={x|x(x-2)<0},B={x||x|≤1},则下列阴影部分表示的集合是( )

| A. | (0,1] | B. | (-2,-1)∪[0,1] | C. | [-1,0]∪(1,2) | D. | [-1,2) |