题目内容
2．$\overrightarrow a=（-2，1），\overrightarrow b=（tanα，-1），且\overrightarrow a∥\overrightarrow b，则\frac{sinα+cosα}{sinα-cosα}$=3．分析 根据向量垂直坐标运算关系建立等式，即可求解．
解答 解：由题意，$\overrightarrow{a}∥\overrightarrow{b}$，
∴tanα=2，
则$\frac{sinα+cosα}{sinα-cosα}$=$\frac{tanα+1}{tanα-1}$=$\frac{2+1}{2-1}$=3．
故答案为：3．
点评 本题考查了“弦化切”及同角三角函数基本关系式，考查了计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．若函数f（x）=x+$\frac{1}{3}$e2x+aex在（-∞，+∞）单调递增，则a的取值范围是（ ）
| A． | $[-\frac{{2\sqrt{6}}}{3}，+∞）$ | B． | $[\frac{{2\sqrt{6}}}{3}，+∞）$ | C． | $[-\frac{{2\sqrt{6}}}{3}，\frac{{2\sqrt{6}}}{3}]$ | D． | $（-\frac{{2\sqrt{6}}}{3}，\frac{{2\sqrt{6}}}{3}）$ |
14．设函数f（x）=|x+2|+|x-a|的图象关于直线x=1对称，则a的值为（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
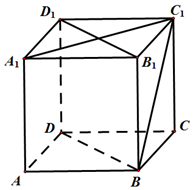如图，已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1，BD，BC1，B1D1，A1C1分别为各个面的对角线；
如图所示，四棱锥P-ABCD的底面积ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=$\sqrt{3}$