题目内容
在D上的函数f(x),如果满足:对?x∈D,存在常数M>0,都有|f(x)|<M成立,则称f(x)是D上的有界函数.则下列定义在R上的函数中,不是有界函数的是( )
| A、f(x)=sinx2 | ||||
B、f(x)=
| ||||
| C、f(x)=-21-|x| | ||||
| D、f(x)=-log2(1+|x|) |
考点:函数的值域
专题:函数的性质及应用
分析:根据有界函数的定义容易判断A,B,C的三个函数都是有界函数,所以不是有界函数的是D.
解答:
解:存在常数2,使|sinx2|<2,∴f(x)=sinx2是有界函数;
存在常数2,使|
|<2,∴f(x)=
是有界函数;
∵1-|x|≤1,∴0<21-|x|≤2,∴|-21-|x||≤2,∴存在常数3使|-21-|x||<3,∴f(x)=-21-|x|是有界函数;
∵1+|x|≥1,∴log2(1+|x|)≥0,∴|-log2(1+|x|)|≥0,∴不存在常数M,使:|-log2(1+|x|)|<M,所以f(x)=-log2(1+|x|)不是有界函数.
故选D.
存在常数2,使|
| 1 | ||
|
| 1 | ||
|
∵1-|x|≤1,∴0<21-|x|≤2,∴|-21-|x||≤2,∴存在常数3使|-21-|x||<3,∴f(x)=-21-|x|是有界函数;
∵1+|x|≥1,∴log2(1+|x|)≥0,∴|-log2(1+|x|)|≥0,∴不存在常数M,使:|-log2(1+|x|)|<M,所以f(x)=-log2(1+|x|)不是有界函数.
故选D.
点评:考查对有界函数定义的理解,正弦函数的取值范围,指数函数与对数函数的单调性与值域.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 ABC-A1B1C1是各棱长均相等的正三棱柱,D是侧棱CC1的中点.求证:平面AB1D⊥平面ABB1A1.
ABC-A1B1C1是各棱长均相等的正三棱柱,D是侧棱CC1的中点.求证:平面AB1D⊥平面ABB1A1.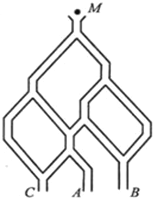 如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.