Question

设实数x，y满足约束条件

x-y-2≤0 x+2y-5≥0 y-2≤0

，则μ=

xy

x2+y2

的取值范围是

 

．

Answer 1

考点：简单线性规划

专题：数形结合,转化思想

分析：由约束条件作出可行域，令z=

1

μ

=

x2+y2

xy

=

1

y x

+

y

x

，由

y

x

的几何意义求出其范围，结合“对勾函数”的单调性求出z的范围，取倒数后得答案．

解答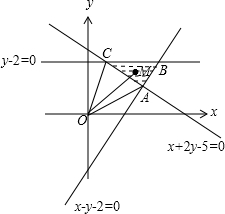： 解：由约束条件

x-y-2≤0 x+2y-5≥0 y-2≤0

作出可行域如图阴影部分所示：
令z=

1

μ

=

x2+y2

xy

=

1

y x

+

y

x

，
则z≥2，当且仅当

y

x

=1时，z最小，最小值为2．
其中

y

x

可以看作是原点（0，0）与可行域内一点（x，y）连线OM的斜率．
其最大值为2，最小值为

1

3

，
由z（2）=

1

2

+2=

5

2

，z（

1

3

）=

1

1 3

+

1

3

=

10

3

，
因此z=

x2+y2

xy

的最大值为

10

3

．
则目标函数z=

x2+y2

xy

的取值范围是[2，

10

3

]．
∴μ=

xy

x2+y2

的取值范围是[

3

10

，

1

2

]．
故答案为：[

3

10

，

1

2

]．

点评：本题考查线性规划知识，考查了数学转化思想方法，考查了数形结合的解题思想方法，训练了利用“对勾函数”的单调性求最值，是有一定难度题目．