题目内容

15．设定点F1（0，2），F2（0，-2），动点P满足条件$|{P{F_1}}|+|{P{F_2}}|=a+\frac{4}{a}（a＞0）$，则点P的轨迹是（　　）
A．椭圆B．线段C．不存在D．椭圆或线段

分析 定点F1（0，2），F2（0，-2），动点P满足条件$|{P{F_1}}|+|{P{F_2}}|=a+\frac{4}{a}（a＞0）$，利用基本不等式的性质可得：|PF1|+|PF2|≥4，当且仅当a=2时取等号．即可得出轨迹方程．

解答 解：∵定点F1（0，2），F2（0，-2），动点P满足条件$|{P{F_1}}|+|{P{F_2}}|=a+\frac{4}{a}（a＞0）$，
∴|PF1|+|PF2|≥2$\sqrt{a×\frac{4}{a}}$=4，当且仅当a=2时取等号．
①|PF1|+|PF2|＞4=|F1F2|，其轨迹为椭圆．
②|PF1|+|PF2|=4=|F1F2|，其轨迹为线段F1F2．
则点P的轨迹是椭圆或线段．
故选：D．

点评 本题考查了椭圆的定义、基本不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
5．某几何体的三视图如图所示，若可放入一球于其内部且与其各面相切，则该几何体的表面积为（　　）
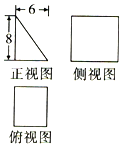
A．96B．144C．192D．240
6．在某次数学趣味活动中，每位参加者需从所有的“三位递增数”中随机抽取1个数，且只能抽取一次．（若n是一个三位正整数，且n的个位数字大于十位数字，十位数字大于百位数字，则称n为“三位递增数”如137，359，567等）得分规则如下：若抽取的“三位递增数”的三个数字之积不能被5整除，参加者得0分；若能被5整除，但不能被10整除，得-1分；若能被10整除，得1分．已知某同学甲参加活动，求甲得分X的分布列．
3．计算$\frac{2+2i}{i}+\frac{1+i}{1-i}$．
10．已知函数$f（x）=\left\{\begin{array}{l}（1-2a）x+5（x≤12）\\{a^{x-13}}（x＞12）\end{array}\right.$，若数列{an}满足an=f（n），n∈N+，且对任意的两个正整数m，n（m≠n），都有（m-n）（am-an）＜0，则实数a的取值范围是（$\frac{1}{2}$，$\frac{2}{3}$）．
20．已知函数y=f（x）（x∈R）满足f（x）=2x+1，在数列{an}，a1=1，an+1=f（an）-1（n∈N*），数列{bn}为等差数列，首项b1=1，公差为2．
（1）求数列{an}，{bn}的通项公式；
（2）令${c_n}=\frac{b_n}{a_n}$（n∈N*），求{cn}的前n项和Tn．
7．设集合An={1，2，3，…，n}（n∈N*，n≥3），记An中的元素组成的非空子集为$A_i^'$（i∈N*，i=1，2，3，…，2n-1），对于?i∈{1，2，3，…，2n-1}，$A_i^'$中的最小元素和为Sn，则S5=（　　）
A．32B．57C．75D．480
4．有6个零件，其中4个一等品，2个二等品，若从这6个零件中任意取2个，那么至少有1个一等品的概率是$\frac{14}{15}$．
5．已知$|{\overrightarrow a}|=|{\overrightarrow b}|=|\overrightarrow a+\overrightarrow b|=2$
（1）求$\overrightarrow a$与$\overrightarrow b$的夹角；
（2）求证：$（{\overrightarrow a+2\overrightarrow b}）⊥\overrightarrow a$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网