题目内容
△ABO中,
=
,
=
,且|
|=|
|,设
=
+
,
=
+
,
=
+
(1)求证:A,B,C,D,E五点共线,
(2)指出|
|,|
|,|
|的最小者,并说明理由.
| OA |
| e1 |
| OB |
| e2 |
| e1 |
| e2 |
| OC |
| 1 |
| 2 |
| e1 |
| 1 |
| 2 |
| e2 |
| OD |
| 1 |
| 3 |
| e1 |
| 2 |
| 3 |
| e2 |
| OE |
| 1 |
| 4 |
| e1 |
| 3 |
| 4 |
| e2 |
(1)求证:A,B,C,D,E五点共线,
(2)指出|
| OC |
| OD |
| OE |
考点:平面向量的基本定理及其意义,向量的模
专题:平面向量及应用
分析:(1)由已知中△ABO中,
=
,
=
,
=
+
,可得
=2
,A,B,C三点共线,同理由
=
+
,
=
+
可得A,B,D三点共线,A,B,E三点共线,进而A,B,C,D,E五点共线,
(2)由|
|=|
|,故△ABO为等腰三角形,则根据点到直线的距离,垂线段最短,可得答案.
| OA |
| e1 |
| OB |
| e2 |
| OC |
| 1 |
| 2 |
| e1 |
| 1 |
| 2 |
| e2 |
| AB |
| AC |
| OD |
| 1 |
| 3 |
| e1 |
| 2 |
| 3 |
| e2 |
| OE |
| 1 |
| 4 |
| e1 |
| 3 |
| 4 |
| e2 |
(2)由|
| e1 |
| e2 |
解答:
证明:(1)∵△ABO中,
=
,
=
,
=
+
,
∴
=
-
=
-
,
=
-
=
(
-
),
∴
=2
,
∴A,B,C三点共线,
同理由
=
+
可得:
=3
,
∴A,B,D三点共线,
由
=
+
可得:
=4
,
∴A,B,E三点共线,
综上,A,B,C,D,E五点共线,
(2)由|
|=|
|,
故△ABO为等腰三角形,
由(1)知,C,D,E分别为AB边的中点,三等分点和四等分点,且OC⊥AB,
根据点到直线的距离,垂线段最短,可得|
|最小.
| OA |
| e1 |
| OB |
| e2 |
| OC |
| 1 |
| 2 |
| e1 |
| 1 |
| 2 |
| e2 |
∴
| AB |
| OB |
| OA |
| e2 |
| e1 |
| AC |
| OC |
| OA |
| 1 |
| 2 |
| e2 |
| e1 |
∴
| AB |
| AC |
∴A,B,C三点共线,
同理由
| OD |
| 1 |
| 3 |
| e1 |
| 2 |
| 3 |
| e2 |
| AB |
| AD |
∴A,B,D三点共线,
由
| OE |
| 1 |
| 4 |
| e1 |
| 3 |
| 4 |
| e2 |
| AB |
| AE |
∴A,B,E三点共线,
综上,A,B,C,D,E五点共线,
(2)由|
| e1 |
| e2 |
故△ABO为等腰三角形,
由(1)知,C,D,E分别为AB边的中点,三等分点和四等分点,且OC⊥AB,
根据点到直线的距离,垂线段最短,可得|
| OC |
点评:本题考查的知识点是向量共线的充要条件,向量模的比较,难度不大,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
把五进制数33(5)化成二进制数是( )
| A、100100(2) |
| B、10010(2) |
| C、1010(2) |
| D、10100(2) |
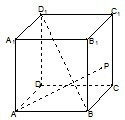 如图,正方体ABCD-A1B1C1D1的棱长为1,点P在侧面CBB1C1及其边界上运动,并且总保持B1P∥平面A1BD,则动点P的轨迹的长度是
如图,正方体ABCD-A1B1C1D1的棱长为1,点P在侧面CBB1C1及其边界上运动,并且总保持B1P∥平面A1BD,则动点P的轨迹的长度是