已知圆O:x2+y2=4上到直线l:x+y=a的距离等于1的点恰有3个.则实数a的值为( )A．2$\sqrt{2}$B．$\sqrt{2}$C．-$\sqrt{2}$或$\sqrt{2}$D．-2$\sqrt{2}$或2$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．已知圆O：x²+y²=4上到直线l：x+y=a的距离等于1的点恰有3个，则实数a的值为（　　）

A．

2$\sqrt{2}$

B．

$\sqrt{2}$

C．

-$\sqrt{2}$或$\sqrt{2}$

D．

-2$\sqrt{2}$或2$\sqrt{2}$

分析由题意可得圆心（0，0）到直线l：x+y=a的距离d满足d=1，根据点到直线的距离公式求出d，再解绝对值方程求得实数a的值．

解答解：因为圆上的点到直线l的距离等于1的点至少有2个，所以圆心到直线l的距离d=1，
即d=$\frac{|-a|}{\sqrt{2}}$=1，解得a=±$\sqrt{2}$．
故选：C．

点评本题主要考查直线和圆的位置关系，点到直线的距离公式，绝对值方程的解法，属于基础题．

练习册系列答案

10．设向量$\overrightarrow{a}$=（2cosx，1），向量$\overrightarrow{b}$=$（\sqrt{3}cosx，\;\;sin2x-\sqrt{3}）$，函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
（Ⅰ）若$α∈（\frac{π}{2}，\;π）$，且sinα=$\frac{5}{13}$，求$f（\frac{α}{2}）$的值；
（Ⅱ）已知△ABC的三内角A，B，C的对边分别为a，b，c，若a=2$\sqrt{3}$，b=3$\sqrt{2}$，f（A）=1，求c．

7．已知以F为焦点的抛物线y²=4x上的两点A，B满足$\overrightarrow{AF}$=2$\overrightarrow{FB}$，则弦AB中点到抛物线准线的距离为$\frac{9}{4}$．

14．若函数f（x）满足：在定义域D内存在实数x₀，使得f（x₀+1）=f（x₀）+f（1）成立，则称函数f（x）为“1的饱和函数”．给出下列四个函数：①f（x）=$\frac{1}{x}$；②f（x）=2^x；③f（x）=lg（x²+2）；④f（x）=cos（πx）．其中是“1的饱和函数”的所有函数的序号为（　　）

4．已知函数f（x）=|x-a|，a∈R
（Ⅰ）当a=1时，求f（x）≥|x+1|+1的解集；
（Ⅱ）若不等式f（x）+3x≤0的解集包含{x|x≤-1}，求a的取值范围．

11．已知函数f（x）=sin（2x-$\frac{π}{2}$）（x∈R）下列结论错误的是（　　）

	A．	函数f（x）的最小正周期为π		B．	函数f（x）是偶函数
	C．	函数f（x）在区间[0，$\frac{π}{2}$]上是增函数		D．	函数f（x）的图象关于直线x=$\frac{π}{4}$对称

8．已知变量x、t满足约束条件$\left\{\begin{array}{l}{x+2y≥2}\\{2x+y≤4}\\{4x-y≥-1}\end{array}\right.$，则目标函数z=3x-y的最大值是（　　）

9．

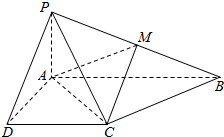已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且$PA=AD=DC=\frac{1}{2}$，AB=1，M是PB的中点．
（1）求AC与PB所成的角的余弦值；
（2）求PC与平面AMC所成角的正弦值．

试题分类