题目内容
18.3名同学分别报名参加学校的足球队,篮球队,乒乓球队,排球队,每人限报其中的一个运动队,不同报法的种数是( )| A. | 34 | B. | 43 | C. | 24 | D. | 12 |
分析 根据题意,易得3名同学中每人有4种报名方法,由分步计数原理计算可得答案.
解答 解:因为3名同学分别报名参加学校的足球队,篮球队,乒乓球队,排球队,
每人限报其中的一个运动队,由分步乘法计数得到为43,
故选B
点评 本题考查分步计数原理的运用,解题时注意题干条件中“每人限报其中的一个运动队”.

练习册系列答案
相关题目
8.如图,三菱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B-PA-C的大小等于( )
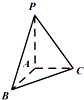

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
9.某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
(1)求广告费支出x与销售额y回归直线方程$\hat y$=bx+a(a,b∈R);
已知b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
已知b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
7.设A、B为两个独立事件,若P(A)=0.4,P(A∪B)=0.7.则P(B)=( )
| A. | 0.6 | B. | 0.5 | C. | 0.4 | D. | 0.3 |
8.若函数f(x)=ax2+ax-1对?x∈R都有f(x)<0恒成立,则实数a的取值范围是( )
| A. | -4<a≤0 | B. | a<-4 | C. | -4<a<0 | D. | a≤0 |