Question

11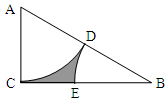．如图，在Rt△ACB中，∠ACB=90°，AB=2AC，分别以A、B为圆心，AC的长为半径作扇形ACD和扇形BDE，D在AB上，E在BC上．在△ACB中任取一点，这一点恰好在图中阴影部分的概率是（　　）

• A． 1-$\frac{{\sqrt{3}π}}{6}$
• B． $\frac{{\sqrt{3}π}}{6}$
• C． 1-$\frac{π}{4}$
• D． $\frac{π}{4}$

Answer 1

分析 设AC=1，求出S_△ABC=$\frac{1}{2}$AC•BC=$\frac{\sqrt{3}}{2}$，再求出S_阴影部分=$\frac{\sqrt{3}}{2}$-$\frac{π}{4}$，利用几何概型的公式解答即可．

解答 解：设AC=1，在Rt△ACB中，∠ACB=90°，AB=2AC=2，
∴S_△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$，
∵分别以A、B为圆心，AC的长为半径作扇形ACD和扇形BEF，
∴扇形ACD+扇形BEF的面积等于以1为半径的圆的面积的四分之一，
∴S_扇形ACD+S_扇形BDE=$\frac{π}{4}$，
∴S_阴影部分=$\frac{\sqrt{3}}{2}$-$\frac{π}{4}$，
∴在△ACB中任取一点，这一点恰好在图中阴影部分的概率是=$\frac{\frac{\sqrt{3}}{2}-\frac{π}{4}}{\frac{\sqrt{3}}{2}}$=1-$\frac{\sqrt{3}π}{6}$
故选：A

点评 本题考查了几何概型的概率公式的运用以及利用定积分求曲边梯形的面积的方法．