题目内容
如图,
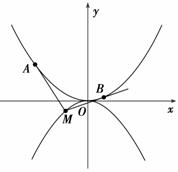
抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1- 时,切线MA的斜率为-
时,切线MA的斜率为-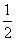 .
.
(1)求p的值;
(2)当M在C 2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
解析:(1)因为抛物线C1:x2=4y上任意一点(x,y )的切线斜率为y′=
)的切线斜率为y′=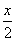 ,且切线MA的斜率为-
,且切线MA的斜率为-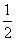 ,所以A点坐标为
,所以A点坐标为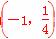 ,故切线MA的方程为y=-
,故切线MA的方程为y=-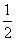 (x+1)+
(x+1)+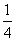 .
.
因为点M(1- ,y0)在切线MA及抛物线C2上,于是
,y0)在切线MA及抛物线C2上,于是
y0=-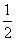 (2-
(2- )+
)+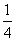 =-
=-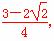 ,①
,①
y0=-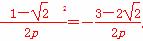 .②
.②
由①②得p=2.
(2)设N( x,y),A
x,y),A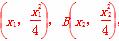 ,x1≠x2,
,x1≠x2,
由N为线段AB中点知
x=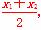 ,③
,③
y=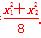 .④
.④
切线MA、MB的方程为
y=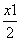 (x-x1)+
(x-x1)+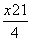 ,⑤
,⑤
y= (x-x2)+
(x-x2)+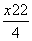 .⑥
.⑥
由⑤⑥得MA,MB的交点M(x0,y0)的坐标为
x0=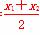
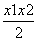 ,y0=
,y0=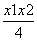 .
.
因为点M(x0,y0)在C2上,即x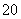 =-4y0,
=-4y0,
所以x1x2=-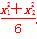 .⑦
.⑦
由③④⑦得x2=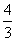 y,x≠0.
y,x≠0.
当x1=x2时,A,B重合于原点O,AB中点N为O,坐标满足x2=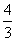 y.
y.
因此AB中点N的轨迹方程为x2=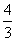 y.
y.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
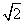 .记动点P的轨迹为W.
.记动点P的轨迹为W.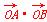 的最小值.
的最小值.
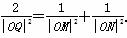 请将n表示为m的函数.
请将n表示为m的函数. )
)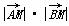 cos2 θ=3.
cos2 θ=3.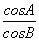 =
=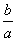 =
=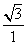 .
. 上,∠PAB=θ,用θ的三角函数表示△PAC的面积,并求△PAC面积最大值.
上,∠PAB=θ,用θ的三角函数表示△PAC的面积,并求△PAC面积最大值.