题目内容
已知函数f(x)=Asin2(ωx+φ)(A>0,ω>0,0<φ<
,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求φ;
(2)计算f(1)+f(2)+…+f(2014)的值.
| π |
| 2 |
(1)求φ;
(2)计算f(1)+f(2)+…+f(2014)的值.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的化简求值
专题:三角函数的图像与性质
分析:(1)根据振幅、周期性、过定点确定其解析式;
(2)利用周期性进行求解.
(2)利用周期性进行求解.
解答:
解:(1)y=Asin2(ωx+φ)=
-
cos(2ωx+2φ),
∵y=f(x)的最大值为2,A>0.
∴A=2.
又∵其图象相邻两对称轴间的距离为2,ω>0,
∴
=2×2,ω=
,
∴f(x)=1-cos(
x+2φ)=1-cos(
x+2φ),
∵y=f(x)过(1,2)点,
∴cos(
+2φ)=-1,
∴
+2φ=2kπ+π,k∈Z,
∴2φ=2kπ+
,k∈Z,
∴φ=kπ+
,k∈Z,
又∵0<φ<
,
∴φ=
.
(2)根据(1)知,函数的周期为4,
∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又∵y=f(x)的周期为4,2014=4×503+2,
∴f(1)+f(2)+…+f(2014)=4×503+f(1)+f(2)=2012+3=2015.
| A |
| 2 |
| A |
| 2 |
∵y=f(x)的最大值为2,A>0.
∴A=2.
又∵其图象相邻两对称轴间的距离为2,ω>0,
∴
| 2π |
| 2ω |
| π |
| 4 |
∴f(x)=1-cos(
| π |
| 2 |
| π |
| 2 |
∵y=f(x)过(1,2)点,
∴cos(
| π |
| 2 |
∴
| π |
| 2 |
∴2φ=2kπ+
| π |
| 2 |
∴φ=kπ+
| π |
| 4 |
又∵0<φ<
| π |
| 2 |
∴φ=
| π |
| 4 |
(2)根据(1)知,函数的周期为4,
∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又∵y=f(x)的周期为4,2014=4×503+2,
∴f(1)+f(2)+…+f(2014)=4×503+f(1)+f(2)=2012+3=2015.
点评:本题重点考查了三角恒等变换公式、三角公式、函数的周期性等知识,属于中档题,解题关键是掌握三角函数值在各个象限内的符号:一全正,二正弦,三两切,四余弦.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
若函数f(x)=|sinx|的图象与y=kx仅有三个公共点且横坐标分别为α,β,r(α<β<r)则下列命题正确的是( )
| A、α=0 |
| B、β∈(0,π) |
| C、r=tanr |
| D、k=-cosr |
 如图,四棱柱A1B1C1D1-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ABC=90°,BC1=B1C,
如图,四棱柱A1B1C1D1-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ABC=90°,BC1=B1C,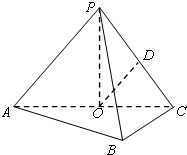 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC= 如图①,有一个长方形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).
如图①,有一个长方形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).