题目内容
若函数f(x)=|sinx|的图象与y=kx仅有三个公共点且横坐标分别为α,β,r(α<β<r)则下列命题正确的是( )
| A、α=0 |
| B、β∈(0,π) |
| C、r=tanr |
| D、k=-cosr |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:首先,根据题意,画出图象,然后,对交点情况进行讨论.
解答:
解:如图所示:

∵函数f(x)=|sinx|的图象与y=kx仅有三个公共点,
且α<β<r,
∴-
<α<β<r=0,或0=α<β<r<
,
不妨设0=α<β<r<
,
∵直线与 y=-sinx 相切,
∴k=-
,同时,由 y'=-cosx,
∴k=-cosγ,
因此,-
=-cosγ,
∴γ=tanγ.
故选:C.

∵函数f(x)=|sinx|的图象与y=kx仅有三个公共点,
且α<β<r,
∴-
| 3π |
| 2 |
| 3π |
| 2 |
不妨设0=α<β<r<
| 3π |
| 2 |
∵直线与 y=-sinx 相切,
∴k=-
| sinγ |
| γ |
∴k=-cosγ,
因此,-
| sinγ |
| γ |
∴γ=tanγ.
故选:C.
点评:本题重点考查了三角函数图象与性质、三角函数图象变换等知识,属于中档题.解题关键是数形结合思想在解题中的应用.

练习册系列答案
相关题目
下面能得出△ABC为锐角三角形的条件是( )
A、sinA+cosA=
| ||||
| B、tanA+tanB+tanC>0 | ||||
C、b=3,c=3
| ||||
D、
|
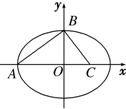 如图,A、B、C分别为椭圆
如图,A、B、C分别为椭圆 有根木料长为6米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,问怎样利用木料,才能使光线通过的窗框面积最大(中间木档的面积可忽略不计).
有根木料长为6米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,问怎样利用木料,才能使光线通过的窗框面积最大(中间木档的面积可忽略不计).