题目内容
18.△ABC与△DEF内接于圆O,∠A,∠B,∠C,∠D的对边分别为a、b、c、d,其中a=c=10$\sqrt{2}$,B=120°,D=45°,则d=20.分析 由已知及余弦定理可求b,利用正弦定理可得$\frac{b}{sinB}=2R$=$\frac{d}{sinD}$,从而计算可求d的值.
解答 解:△ABC中,∵a=c=10$\sqrt{2}$,B=120°,
∴由余弦定理可得:b=$\sqrt{{a}^{2}+{c}^{2}-2accosB}$=$\sqrt{200+200-2×10\sqrt{2}×10\sqrt{2}×(-\frac{1}{2})}$=10$\sqrt{6}$,
∴设圆半径为R,由正弦定理$\frac{b}{sinB}=2R$=$\frac{d}{sinD}$,可得:$\frac{10\sqrt{6}}{\frac{\sqrt{3}}{2}}$=2R=$\frac{d}{\frac{\sqrt{2}}{2}}$,
∴解得:d=20.
故答案为:20.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了转化思想和计算能力,属于中档题.

练习册系列答案
相关题目
6.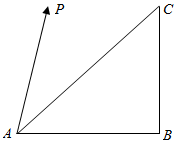 等腰直角△ABC的直角顶点为B,两条直角边长都为1,点P为三角形所在平面内的一点,若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,且|$\overrightarrow{AP}$|=1,则λ的取值范围为( )
等腰直角△ABC的直角顶点为B,两条直角边长都为1,点P为三角形所在平面内的一点,若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,且|$\overrightarrow{AP}$|=1,则λ的取值范围为( )
 等腰直角△ABC的直角顶点为B,两条直角边长都为1,点P为三角形所在平面内的一点,若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,且|$\overrightarrow{AP}$|=1,则λ的取值范围为( )
等腰直角△ABC的直角顶点为B,两条直角边长都为1,点P为三角形所在平面内的一点,若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$,且|$\overrightarrow{AP}$|=1,则λ的取值范围为( )| A. | [-1,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | [-$\sqrt{2}$,1] | D. | [-1,1] |
3.执行如下程序框图,则输出结果为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.已知b为如图所示的程序框图的输出结果,则b=( )


| A. | 9 | B. | 7 | C. | 5 | D. | 4 |