题目内容
14.定义在R上的函数f(x)满足:①f(x)是偶函数;
②f(x-1)是奇函数;
③f(x)=$\left\{\begin{array}{l}{0,x=0}\\{lnx,x∈(0,1]}\end{array}\right.$.
则方程f(x)+2=f(2)在区间(-2,10)内的所有实根之和为( )
| A. | 22 | B. | 24 | C. | 26 | D. | 28 |
分析 根据f(x)满足的条件①②便可得出f(x)为周期为4的周期函数,并且可得到f(x)的图象关于y轴和点(-1,0)对称,根据f(x)在(0,1]上的解析式可画出f(x)在(0,1]上的图象,根据f(x)的对称性和周期便可画出f(x)在(-2,10)上的图象,并且可以求出f(2)=0,从而得出f(x)=-2.再画出y=-2的图象,该图象和f(x)图象的交点横坐标便是f(x)=-2的解,结合图象即可求出f(x)=-2的所有实根之和,从而找出正确选项.
解答 解:f(x)是偶函数,f(x-1)为奇函数;
∴f(x)的图象关于y轴和点(-1,0)对称,且f(x)=f(-x)=f[(-x+1)-1]=-f(x-2)=f(x-4);
∴f(x)是周期为4的周期函数;
可作f(x)在(0,1]上的图象,然后作该图象关于y轴的对称图象便可得出f(x)在[-1,0)上的图象,再作关于点(-1,0)的对称图象便可得出在(-2,1]上的图象,再作该图象关于y轴的对称图象,便可得出f(x)在[1,2)上的图象;
∴可得到f(x)在一个周期(-2,2)上的图象,从而得出f(x)在(-2,10)上的图象如下所示:
f(2)=-f(2-2)=-f(0)=0;
∴f(x)+2=0;
即f(x)=-2;
如图所示,f(x)和y=-2交点的横坐标为方程f(x)=-2的解;
根据图象$\frac{{x}_{1}+{x}_{2}}{2}=0,\frac{{x}_{3}+{x}_{4}}{2}=4,\frac{{x}_{5}+{x}_{6}}{2}=8$;
∴x1+x2+x3+x4+x5+x6=24.
故选:B.
点评 考查奇函数和偶函数的定义,以及周期函数的定义,方程的解和函数图象交点坐标的关系,以及奇函数、偶函数,和周期函数的对称性,数形结合解题的方法.

 快捷英语周周练系列答案
快捷英语周周练系列答案| 答对题目数 | 小于8 | 8 | 9 | 10 |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
(Ⅱ)从答对题目数不少于8道的实习期司机中任意选出两人做进一步的调查,求选出的两人中至少有一名女实习期司机的概率.
| A. | 10($\sqrt{3}$-1) | B. | 10($\sqrt{2}$+1) | C. | 10($\sqrt{2}$-1) | D. | 10($\sqrt{3}$+1) |
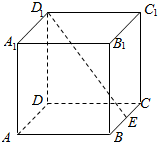 姐图,在正方体ABCD-A1B1C1D1中,E为BC的中点,点P在正方体表面上移动,且满足B1P⊥D1E,则点B1和点P构成的图形是( )
姐图,在正方体ABCD-A1B1C1D1中,E为BC的中点,点P在正方体表面上移动,且满足B1P⊥D1E,则点B1和点P构成的图形是( )| A. | 三角形 | B. | 四边形 | C. | 曲边形 | D. | 五边形 |