题目内容
17.已知函数f(x)=-x2+2x,g(x)=|f(x)|.(1)求f(x)在区间[-1,2]上的最小值;
(2)作出函数g(x)的图象,并根据图象写出其单调减区间;
(3)若函数y=g(x)-log2m至少有三个零点,求实数m的取值范围.
分析 (1)根据二次函数的性质即可求出函数的最小值,
(2)先化为分段函数,再画图即可,并根据图象写出其单调减区间,
(3)由题意可知y=g(x)与y=log2m的两图象至少有三个交点,结合图象可得.
解答 解:(1)∵f(x)在[-1,1]上是增函数,在(1,2]上是减函数,
∴f(x)min=f(-1)=-1-2=-3.
(2)∵$g(x)=\left\{\begin{array}{l}-{x^2}+2x,0≤x≤2\\{x^2}-2x,x<0或x>2\end{array}\right.$
∴作出函数g(x)的图象如图,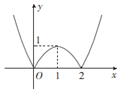
故函数g(x)的单调递减区间是(-∞,0)和(1,2).
(3)由题意可知y=g(x)与y=log2m的两图象至少有三个交点,
所以根据(2)中图象可得0<log2m≤1,
∴1<m≤2,
即m∈(1,2].
点评 本题考查了二次函数的图象和性质以及绝对值函数图象的画法和参数的取值范围,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列函数中为偶函数的是( )
| A. | y=sin|x| | B. | y=sin2x | C. | y=-sinx | D. | y=sinx+1 |
6.中央电视台第一套节目午间新闻的播出时间是每天中午12:00到12:30,在某星期天中午的午间新闻中将随机安排播出时长5分钟的有关电信诈骗的新闻报道.若小张于当天12:20打开电视,则他能收看到这条新闻的完整报道的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
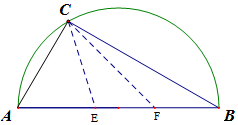 如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.