��Ŀ����
2����֪����f��x��=$\left\{\begin{array}{l}{sinx��sinx��cosx}\\{cosx��sinx��cosx}\end{array}\right.$������f��x������������С������Ϊ2��
�������ֵ1����Сֵ-1
�۶Գ���Ϊֱ��$x=k��+\frac{��}{4}��{k��Z}��$
�ܶԳ�����Ϊ$��{k��+\frac{��}{4}��0}����k��Z��$
����$[{\frac{��}{2}����}]$�ϵ����ݼ�
������ȷ����������Ǣ٢ۢݣ�����������ȷ�������Ŷ����ϣ�
���� �⣺��������f��x��=$\left\{\begin{array}{l}{sinx��sinx��cosx}\\{cosx��sinx��cosx}\end{array}\right.$��ͼ�����ν�Ͽɵý��ۣ�
��� �⣺�ߺ���f��x��=$\left\{\begin{array}{l}{sinx��sinx��cosx}\\{cosx��sinx��cosx}\end{array}\right.$����ʾȡsinx��cosx��ֵ��С�ģ�����ͼ����ͼ�к�ɫ������ʾ��
��sinx��cosx��������Ϊ2�еĺ�������f��x������С������Ϊ2�У��ʢ���ȷ��
���f��x����ͼ��ɵ�f��x�������ֵΪ1����СֵΪ-$\frac{\sqrt{2}}{2}$���ʢڴ���
���f��x����ͼ��ɵ�f��x������СֵΪ-$\frac{\sqrt{2}}{2}$��f��x����ͼ��ĶԳ���Ϊֱ��$x=k��+\frac{��}{4}��{k��Z}��$��
�ʢ���ȷ���ܴ���
����f��x����$[{\frac{��}{2}����}]$�ϵ����ݼ����ʢ���ȷ��
�ʴ�Ϊ���٢ۢݣ�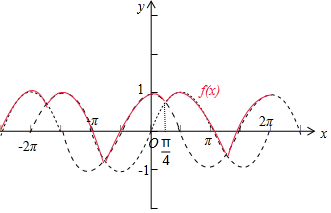
���� ������Ҫ�������Ǻ�����ͼ������ʣ������е��⣮

��ϰ��ϵ�д�
 ������������ϵ�д�
������������ϵ�д�
�����Ŀ
7����֪f��x����g��x����h��x����Ϊһ�κ���������ʵ��x���㣺|f��x��|+|g��x��|+h��x��=$\left\{\begin{array}{l}{4x+2}&{x��2}\\{δ֪}&{-\frac{1}{2}��x��2}\\{-2x+4}&{x��-\frac{1}{2}}\end{array}\right.$����h��x���Ľ���ʽΪ��������
| A�� | 2x+6 | B�� | 6x-2 | C�� | 3x-1 | D�� | x+3 |
14��ֱ��y=kx+1-k����Բ$\frac{x^2}{9}+\frac{y^2}{4}=1$��λ�ù�ϵΪ��������
| A�� | �ཻ | B�� | ���� | C�� | ���� | D�� | ��ȷ�� |
11��������y=x2-mx+1������[1��2]�ϵ�����������ʵ��m��ȡֵ��Χ�ǣ�������
| A�� | ��-�ޣ�2] | B�� | ��-�ޣ�2�� | C�� | ��4��+�ޣ� | D�� | [4��+�ޣ� |