题目内容
11.已知$\overrightarrow{a}$+$\overrightarrow{b}$=2$\overrightarrow{e}$1-8$\overrightarrow{e}$2,$\overrightarrow{a}$-$\overrightarrow{b}$=-8$\overrightarrow{e}$1+16$\overrightarrow{e}$2,其中|$\overrightarrow{e}$1|=|$\overrightarrow{e}$2|=1,$\overrightarrow{e}$1⊥$\overrightarrow{e}$2,则$\overrightarrow{a}$•$\overrightarrow{b}$=-63.分析 由题意可求得$\overrightarrow{a}$=-3$\overrightarrow{e}$1+4$\overrightarrow{e}$2,$\overrightarrow{b}$=5$\overrightarrow{e}$1-12$\overrightarrow{e}$2,从而求$\overrightarrow{a}$•$\overrightarrow{b}$的值.
解答 解:∵$\overrightarrow{a}$+$\overrightarrow{b}$=2$\overrightarrow{e}$1-8$\overrightarrow{e}$2,$\overrightarrow{a}$-$\overrightarrow{b}$=-8$\overrightarrow{e}$1+16$\overrightarrow{e}$2,
∴$\overrightarrow{a}$=$\frac{1}{2}$(2$\overrightarrow{e}$1-8$\overrightarrow{e}$2-8$\overrightarrow{e}$1+16$\overrightarrow{e}$2)=-3$\overrightarrow{e}$1+4$\overrightarrow{e}$2,
$\overrightarrow{b}$=$\frac{1}{2}$(2$\overrightarrow{e}$1-8$\overrightarrow{e}$2+8$\overrightarrow{e}$1-16$\overrightarrow{e}$2)=5$\overrightarrow{e}$1-12$\overrightarrow{e}$2,
又∵|$\overrightarrow{e}$1|=|$\overrightarrow{e}$2|=1,$\overrightarrow{e}$1⊥$\overrightarrow{e}$2,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=(-3$\overrightarrow{e}$1+4$\overrightarrow{e}$2)(5$\overrightarrow{e}$1-12$\overrightarrow{e}$2)
=-15-48=-63,
故答案为:-63.
点评 本题考查了平面向量的化简与运算,同时考查了数量积的运算.

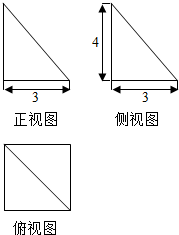
| A. | $\frac{1}{4}π$ | B. | 3π | C. | 4π | D. | $\frac{4}{3}π$ |
| A. | $\overrightarrow{a}•\overrightarrow{b}$=0 | B. | $\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | C. | $\overrightarrow{a}•\overrightarrow{b}$=-|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |