题目内容
17.已知函数h(x)的图象与函数g(x)=ex的图象关于直线y=x对称,点A在函数f(x)=ax-x2($\frac{1}{e}≤x≤e$,e为自然对数的底数)上,A关于x轴对称的点A'在函数h(x)的图象上,则实数a的取值范围是( )| A. | $[{1,e+\frac{1}{e}}]$ | B. | $[{1,e-\frac{1}{e}}]$ | C. | $[{e-\frac{1}{e},e+\frac{1}{e}}]$ | D. | $[{e-\frac{1}{e},e}]$ |
分析 由题意可得,函数f(x)=x2-ax($\frac{1}{e}$≤x≤e,e为自然对数的底数)与函数h(x)=lnx的图象有交点,即x2-ax=lnx,($\frac{1}{e}$≤x≤e)有解,然后利用导数法,可得实数a取值范围.
解答 解:∵函数h(x)的图象与函数g(x)=ex的图象关于直线y=x对称,∴h(x)=lnx,
若函数f(x)=ax-x2($\frac{1}{e}$≤x≤e,e为自然对数的底数)与h(x)=lnx的图象上存在关于直线y=0对称的点,
则函数f(x)=x2-ax($\frac{1}{e}$≤x≤e,e为自然对数的底数)与函数h(x)=lnx的图象有交点,
即x2-ax=lnx,($\frac{1}{e}$≤x≤e)有解,
即a=x-$\frac{lnx}{x}$,($\frac{1}{e}$≤x≤e)有解,
令y=x-$\frac{lnx}{x}$,($\frac{1}{e}$≤x≤e),
则y′=$\frac{{x}^{2}-1+lnx}{{x}^{2}}$,
当$\frac{1}{e}$≤x<1时,y′<0,函数为减函数,
当1<x≤e时,y′>0,函数为增函数,
故x=1时,函数取最小值1,
当x=$\frac{1}{e}$时,函数取最大值e+$\frac{1}{e}$,
∴实数a取值范围是[1,e+$\frac{1}{e}$],
故选:A
点评 本题考查的知识点是函数图象的交点与方程根的关系,利用导数求函数的最值,是中档题.

练习册系列答案
相关题目
8.数列{an}中,已知a1=1,a2=2,an+2=an+1-an(n∈N*),则a2017=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
5.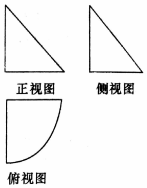 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )
 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )| A. | 2 | B. | π+4 | C. | $\sqrt{2}π+4$ | D. | $({\sqrt{2}+1})π+4$ |
12.设$z=\frac{i}{1-i}$(i为虚数单位),则$\frac{1}{|z|}$=( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
2.在区间[0,1]上随机取两个数,则这两个数之和小于$\frac{3}{2}$的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD