题目内容
已知函数f(x)=1+x-
+
-
+…+
,则下列结论正确的是( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2015 |
| 2015 |
| A、f(x)在(0,1)上恰有一个零点 |
| B、f(x)在(-1,0)上恰有一个零点 |
| C、f(x)在(0,1)上恰有两个零点 |
| D、f(x)在(-1,0)上恰有两个零点 |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用,导数的综合应用
分析:由题意求导f′(x)=1-x+x2-x3+…+x2014=(1-x)(1+x2+…+x2012)+x2014;从而确定函数的单调性,再由函数零点的判定定理求解.
解答:
解:∵f′(x)=1-x+x2-x3+…+x2014
=(1-x)(1+x2+…+x2012)+x2014;
∴f′(x)>0在(-1,0)上恒成立;
故f(x)在(-1,0)上是增函数;
又∵f(0)=1,
f(-1)=1-1-
-
-…-
<0;
故f(x)在(-1,0)上恰有一个零点;
故选B.
=(1-x)(1+x2+…+x2012)+x2014;
∴f′(x)>0在(-1,0)上恒成立;
故f(x)在(-1,0)上是增函数;
又∵f(0)=1,
f(-1)=1-1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2015 |
故f(x)在(-1,0)上恰有一个零点;
故选B.
点评:本题考查了导数的综合应用及函数零点的个数的判断,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知实数x,y满足
,则z=x+y的最小值等于( )
|
| A、0 | B、1 | C、2 | D、3 |
当0<x<1,函数y=x(1-x)的最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
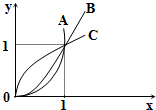 已知幂函数①y=x
已知幂函数①y=x | 1 |
| 2 |
| A、①②③ | B、③①② |
| C、③②① | D、①③② |