题目内容
12.若函数f(x)对任意x∈R,满足f(x-1)=f(x+1),且当x∈[-1,1]时,f(x)=1-x2.函数g(x)=$\left\{\begin{array}{l}{lgx,x>0}\\{-\frac{1}{x},x<0}\end{array}\right.$则函数h(x)=f(x)-g(x)在区间[-11,11]上零点的个数为20.分析 由f(x-1)=f(x+1),得函数的周期是2,由h(x)=f(x)-g(x)=0得f(x)=g(x),作出函数f(x)和g(x)在区间[-11,11]上的图象,利用数形结合判断两个函数的交点个数即可.
解答 解:∵f(x-1)=f(x+1),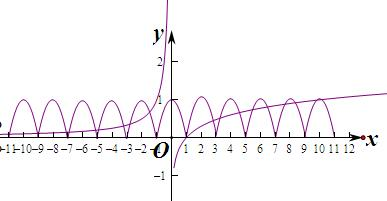
∴f(x)=f(x+2),
即函数f(x)的周期是2,
由h(x)=f(x)-g(x)=0得f(x)=g(x),
∵当x∈[-1,1]时,f(x)=1-x2.
∴作出函数f(x)和g(x)在区间[-11,11]上的图象如图:
由图象知两个函数有20个交点,
故函数的零点个数为20,
故答案为:20
点评 本题主要考查函数与方程的应用,根据条件将函数 转化为两个函数的交点个数问题,利用数形结合是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.盒子中有10张奖券,其中3张有奖,甲、乙先后从中各抽取1张(不放回),记“甲中奖”为A,“乙中奖”为B.
(1)求P(A),P(B),P(AB),P(A|B);
(2)A与B是否相互独立?说明理由.
(1)求P(A),P(B),P(AB),P(A|B);
(2)A与B是否相互独立?说明理由.
2.已知圆A过原点,直线l被圆A截得的弦的中点为M(1,2).弦长2$\sqrt{3}$,则圆A的半径的最小值为( )
| A. | $\frac{2\sqrt{5}}{5}$ | B. | 1 | C. | $\frac{4\sqrt{5}}{5}$ | D. | 2 |