��Ŀ����
3�����嵱a��0ʱ��[a]x=$\left\{\begin{array}{l}{��-a��^{x}��x��0}\\{��-a��^{-x}��x��0}\end{array}\right.$�������ĸ����⣺����a��0��b��0��c��0����[a]cbc=[ab]c��
����a��0��b��0��c��0����[a]cbc=[ab]c��
����a��0��b��0��c��0����acbc=[-ab]c��
����a��0��b��0��c��0����acbc=[-ab]c
���е��������Т٢ۣ�д������������ı�ţ���
���� ���ݷֶκ�������ֵ������ȷ����ֵ���Ӷ��жϣ�
��� �⣺��a��0��b��0��c��0��
��[a]cbc=��-a��cbc��[ab]c=��-ab��c=��-a��cbc���ʢ��棻
��a��0��b��0��c��0��
��[a]cbc=��-a��-cbc��[ab]c=��-ab��-c=��-a��-cb-c���ʢڼ٣�
��a��0��b��0��c��0��
��[-ab]c=��ab��c���ʢ��棻
��a��0��b��0��c��0��
��[-ab]c=��ab��-c���ʢܼ٣�
�ʴ�Ϊ���٢ۣ�
���� ���⿼���˷ֶκ����ı���Ӧ�ü��������۵�˼��Ӧ�ã�

��ϰ��ϵ�д�
 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д�
�����Ŀ
15����֪����f��x���Ķ�����ΪR��������x1��x2����f��x1��-f��x2����x1-x2����f��-3��=-4����ʽf��log${\;}_{\frac{1}{2}}$|3x-1|����log${\;}_{\frac{1}{2}}$|3x-1|-1�Ľ⼯Ϊ��������
| A�� | ��2��+�ޣ� | B�� | ��-�ޣ�2�� | C�� | ��0��1���ȣ�1��2�� | D�� | ��-�ޣ�0���ȣ�0��2�� |
13����֪$\overrightarrow{a}$��$\overrightarrow{b}$Ϊͬһƽ���ڵ�������������$\overrightarrow{a}$=��1��2����|$\overrightarrow{b}$|=$\frac{1}{2}$|$\overrightarrow{a}$|����$\overrightarrow{a}$+2$\overrightarrow{b}$��2$\overrightarrow{a}$-$\overrightarrow{b}$��ֱ����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ��������
| A�� | 0 | B�� | $\frac{��}{4}$ | C�� | $\frac{2��}{3}$ | D�� | �� |
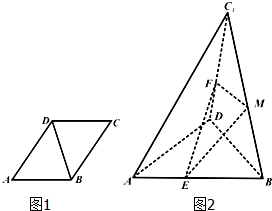 ��֪����ABCD�У�AB=4����BAD=60�㣬������ABCD�ضԽ���BD���ۣ�ʹ��C���۵���C1��λ�ã���E��F��M�ֱ���AB��DC1��BC1���е㣮
��֪����ABCD�У�AB=4����BAD=60�㣬������ABCD�ضԽ���BD���ۣ�ʹ��C���۵���C1��λ�ã���E��F��M�ֱ���AB��DC1��BC1���е㣮