题目内容
设角α的终边过点P(6a,8a)(a≠0),求sinα-cosα的值.
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:根据三角函数的定义进行求解即可.
解答:
解:∵角α的终边过点P(6a,8a)(a≠0),
∴r=
=10|a|,
若a>0,则sinα-cosα=
-
=
-
=
-
=
=
,
若a<0,则sinα-cosα=
-
=-
-(-
)=-
+
=-
=-
,
故sinα-cosα=±
.
∴r=
| (6a)2+(8a)2 |
若a>0,则sinα-cosα=
| 8a |
| 10|a| |
| 6a |
| |10a| |
| 8a |
| 10a |
| 6a |
| 10a |
| 8 |
| 10 |
| 6 |
| 10 |
| 2 |
| 10 |
| 1 |
| 5 |
若a<0,则sinα-cosα=
| 8a |
| 10|a| |
| 6a |
| |10a| |
| 8a |
| 10a |
| 6a |
| 10a |
| 8 |
| 10 |
| 6 |
| 10 |
| 2 |
| 10 |
| 1 |
| 5 |
故sinα-cosα=±
| 1 |
| 5 |
点评:本题主要考查三角函数的定义的应用,注意要对a进行讨论.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
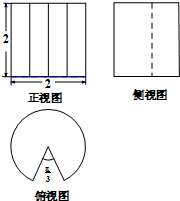
已知某几何体的三视图如图所示,则它的体积是( )

A、
| ||
B、
| ||
| C、π | ||
D、
|
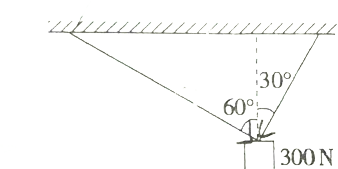 如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.
如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.