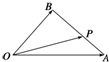
题目内容
在梯形中ABCD，AB∥CD，AB=2CD，M，N分别是CD，AB的中点，设
=
，
=
．
（1）在图上作出向量
+
（不要求写出作法）
（2）请将
用
，
表示．
| AB |
| e1 |
| AD |
| e2 |
（1）在图上作出向量
| 1 |
| 2 |
| e1 |
| e2 |
（2）请将
| MN |
| e1 |
| e2 |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）如图所示，连接NC，在四边形ANCD中，由AB∥CD，AB=2CD，N是AB的中点，可得AN=CD，四边形ANCD是平行四边形，可得
=
+
=
+
．
（2）由M，N分别是CD，AB的中点，可得
=
=-
，
=
，代入
=
+
+
即可得出．
| AC |
| AN |
| AD |
| 1 |
| 2 |
| AB |
| AD |
（2）由M，N分别是CD，AB的中点，可得
| MD |
| 1 |
| 2 |
| CD |
| 1 |
| 4 |
| AB |
| AN |
| 1 |
| 2 |
| AB |
| MN |
| MD |
| DA |
| AN |
解答：
解：（1）如图所示，连接NC，在四边形ANCD中，
∵AB∥CD，AB=2CD，N是AB的中点，
∴AN=CD，
∴四边形ANCD是平行四边形，
∴
=
+
=
+
=
+
．
（2）∵M，N分别是CD，AB的中点，
∴
=
=-
，
=
，
∴
=
+
+
=
-
=
-
．
∵AB∥CD，AB=2CD，N是AB的中点，
∴AN=CD，
∴四边形ANCD是平行四边形，
∴
| AC |
| AN |
| AD |
| 1 |
| 2 |
| AB |
| AD |
| 1 |
| 2 |
| e1 |
| e2 |
（2）∵M，N分别是CD，AB的中点，
∴
| MD |
| 1 |
| 2 |
| CD |
| 1 |
| 4 |
| AB |
| AN |
| 1 |
| 2 |
| AB |
∴
| MN |
| MD |
| DA |
| AN |
=
| 1 |
| 4 |
| AB |
| AD |
=
| 1 |
| 4 |
| e1 |
| e2 |
点评：本题考查了向量的多边形法则、平行四边形的判定与性质、向量共线定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知函数y=f（x）对任意x∈R，恒有（f（x）-sinx）（f（x）-cosx）=0成立，则下列关于函数 y=f（x）的说法正确的是（ ）
| A、最小正周期是2π |
| B、值域是[-1，1] |
| C、是奇函数或是偶函数 |
| D、以上都不对 |
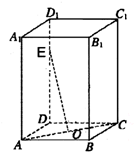如图，在长方体ABCD-A1B1C1D1中，O为AC的中点，设E是棱DD1上的点，且