题目内容
已知二次函数f(x)=ax2+bx+c
(1)若a=1,记函数f(x)在[-1,1]上最大值为M,最小值为m,求M-m≤4时b的取值范围
(2)若f(x)过点(-1,-1)
①是否存在a、b、c,使得2x≤f(x)≤
对于x∈R恒成立,若有,求出f(x)的解析式?若无,说明理由;
②当c=2a+3,关于x的方程log2[f(x)-8a-4]=log2(x+1)(3-x)存在解,求a的范围?
(1)若a=1,记函数f(x)在[-1,1]上最大值为M,最小值为m,求M-m≤4时b的取值范围
(2)若f(x)过点(-1,-1)
①是否存在a、b、c,使得2x≤f(x)≤
| x2+2x+1 |
| 2 |
②当c=2a+3,关于x的方程log2[f(x)-8a-4]=log2(x+1)(3-x)存在解,求a的范围?
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)由题意,f(x)=x2+bx+c,讨论对称轴以确定最值,从而解得;
(2)①由题意b=a+c+1;化恒成立问题为最值问题,从而求解;
②化简f(x)=ax2+bx+c=ax2+(3a+4)x+(2a+3);从而化log2[f(x)-8a-4]=log2(x+1)(3-x)为(a+1)x2+(3a+2)x-6a-4=0,令令F(x)=(a+1)x2+(3a+2)x-6a-4,从而求解.
(2)①由题意b=a+c+1;化恒成立问题为最值问题,从而求解;
②化简f(x)=ax2+bx+c=ax2+(3a+4)x+(2a+3);从而化log2[f(x)-8a-4]=log2(x+1)(3-x)为(a+1)x2+(3a+2)x-6a-4=0,令令F(x)=(a+1)x2+(3a+2)x-6a-4,从而求解.
解答:
解:(1)f(x)=x2+bx+c,
当-1≤-
≤1,即-2≤b≤2时,
,
解得,-2≤b≤2,
当-
>1,即b<-2时,
M=f(-1)=1-b+c,
m=f(1)=1+b+c,
则1-b+c-(1+b+c)≤4,
解得,b≥-2,不成立;
同理当-
<-1,即b>2时,也不成立;
综上所述,-2≤b≤2.
(2)①∵f(x)过点(-1,-1),
∴a-b+c=-1,
即b=a+c+1;
由f(x)-2x=ax2+(b-2)x+c≥0恒成立得,
,
同理,由f(x)≤
恒成立得,
或
,
故当a=
,b=1,c=-
时,上式成立;
故f(x)=
x2+x-
;
②当c=2a+3,b=3a+4;
故f(x)=ax2+bx+c
=ax2+(3a+4)x+(2a+3);
f(x)-8a-4=ax2+(3a+4)x-6a-1,
由log2[f(x)-8a-4]=log2(x+1)(3-x)可得,
-1<x<3,
故f(x)-8a-4=ax2+(3a+4)x-6a-1=(x+1)(3-x),
即(a+1)x2+(3a+2)x-6a-4=0在(-1,3)上有解,
若a+1=0,解得,x=2,成立;
令F(x)=(a+1)x2+(3a+2)x-6a-4,
若-
≤-1或-
≥3,即a>0或a<-1或-1<a<-
时,
F(-1)•F(3)<0,
即((a+1)-(3a+2)-6a-4)(9(a+1)+3(3a+2)-6a-4)<0,
解得a>-
或a<-
故a>0或a<-1或-1<a<-
,
当-1<-
<3,即-
<a<0时,
△=(3a+2)2+4(a+1)(6a+4)≥0
解得,a≥-
或a≤-
,
F(-1)>0或F(3)>0,
即-8a-5>0或12a+11>0,
解得,-
≤a<0,
综上所述,a<-
或-
≤a<0或a>0.
当-1≤-
| b |
| 2 |
|
解得,-2≤b≤2,
当-
| b |
| 2 |
M=f(-1)=1-b+c,
m=f(1)=1+b+c,
则1-b+c-(1+b+c)≤4,
解得,b≥-2,不成立;
同理当-
| b |
| 2 |
综上所述,-2≤b≤2.
(2)①∵f(x)过点(-1,-1),
∴a-b+c=-1,
即b=a+c+1;
由f(x)-2x=ax2+(b-2)x+c≥0恒成立得,
|
同理,由f(x)≤
| x2+2x+1 |
| 2 |
|
|
故当a=
| 1 |
| 2 |
| 1 |
| 2 |
故f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
②当c=2a+3,b=3a+4;
故f(x)=ax2+bx+c
=ax2+(3a+4)x+(2a+3);
f(x)-8a-4=ax2+(3a+4)x-6a-1,
由log2[f(x)-8a-4]=log2(x+1)(3-x)可得,
-1<x<3,
故f(x)-8a-4=ax2+(3a+4)x-6a-1=(x+1)(3-x),
即(a+1)x2+(3a+2)x-6a-4=0在(-1,3)上有解,
若a+1=0,解得,x=2,成立;
令F(x)=(a+1)x2+(3a+2)x-6a-4,
若-
| 3a+2 |
| 2a+2 |
| 3a+2 |
| 2a+2 |
| 8 |
| 9 |
F(-1)•F(3)<0,
即((a+1)-(3a+2)-6a-4)(9(a+1)+3(3a+2)-6a-4)<0,
解得a>-
| 5 |
| 8 |
| 11 |
| 12 |
故a>0或a<-1或-1<a<-
| 11 |
| 12 |
当-1<-
| 3a+2 |
| 2a+2 |
| 8 |
| 9 |
△=(3a+2)2+4(a+1)(6a+4)≥0
解得,a≥-
| 2 |
| 3 |
| 10 |
| 11 |
F(-1)>0或F(3)>0,
即-8a-5>0或12a+11>0,
解得,-
| 2 |
| 3 |
综上所述,a<-
| 11 |
| 12 |
| 2 |
| 3 |
点评:本题考查了二次函数的性质应用,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
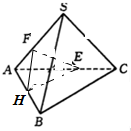 如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为
如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为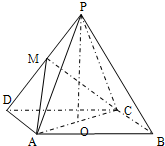 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC,O为AC中点,PO⊥平面ABCD,M为PD中点.若AC=2PO,求二面角P-AB-C的正切值.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC,O为AC中点,PO⊥平面ABCD,M为PD中点.若AC=2PO,求二面角P-AB-C的正切值.