题目内容
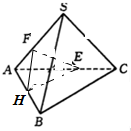 如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为
如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为考点:棱锥的结构特征
专题:空间位置关系与距离
分析:先求出△SBC的面积S△SBC,再证明△HFE∽△SBC,从而求出△HFE的面积.
解答:
 解:如图所示,
解:如图所示,
∵四面体S-ABC的六条棱长都为4,
∴△SBC的面积是S△SBC=
×4×4sin60°=4
;
又∵E为SA的中点,平面EFH∥平面SBC,且平面EFH∩平面ABC=FH,
∴EF∥SB,且EF=
SB,
FH∥BC,且FH=
BC;
∴△HFE∽△SBC,
∴△HFE的面积为
S△SBC=
.
故答案为:
.
 解:如图所示,
解:如图所示,∵四面体S-ABC的六条棱长都为4,
∴△SBC的面积是S△SBC=
| 1 |
| 2 |
| 3 |
又∵E为SA的中点,平面EFH∥平面SBC,且平面EFH∩平面ABC=FH,
∴EF∥SB,且EF=
| 1 |
| 2 |
FH∥BC,且FH=
| 1 |
| 2 |
∴△HFE∽△SBC,
∴△HFE的面积为
| 1 |
| 4 |
| 3 |
故答案为:
| 3 |
点评:本题考查了三棱锥的结构特征的应用问题,也考查了空间中的平行关系的应用问题,是基础题.

练习册系列答案
相关题目
已知在正四面体ABCD中,E、F分别是线段AB和线段CD上一点,且AE=
AB,CF=
CD,则直线DE和BF所成角的余弦值是( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
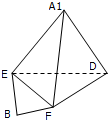 如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.
如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.