题目内容
6．在等腰三角形ABC中，AB=AC，D、E分别为AB、AC上的动点，若$\frac{AD}{AB}$=$\frac{CE}{AC}$=$\frac{1}{3}$，且$\overrightarrow{DE}$•$\overrightarrow{BC}$=8，则|$\overrightarrow{BC}$|=4．分析 建立平面直角坐标系，求出各向量坐标，代入数量积公式计算求出．
解答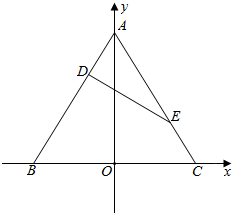 
解：以BC为x轴，BC边上的高为y轴建立平面直角坐标系，如图，设C（a，0），B（-a，0），A（0，b），
∵$\frac{AD}{AB}=\frac{CE}{AC}$=$\frac{1}{3}$，∴D（-$\frac{a}{3}$，$\frac{2b}{3}$），E（$\frac{2a}{3}$，$\frac{b}{3}$），∴$\overrightarrow{DE}$=（a，-$\frac{b}{3}$），$\overrightarrow{BC}$=（2a，0）．
∴$\overrightarrow{DE}•\overrightarrow{BC}$=2a2=8，解得a=2，∴BC=2a=4．
故答案为：4．
点评 本题考查了平面向量的数量积运算，建立坐标系通常可使计算简便．
练习册系列答案
相关题目
如图，单位圆⊙O与x轴正半轴交于点A，角α与β的终边分别与单位圆交于B（xB，yB）、C（xC，yC）两点，且满β-α=$\frac{π}{4}$，其中α为锐角．