题目内容
3.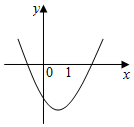 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )| A. | 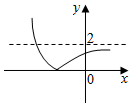 | B. | 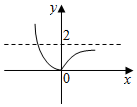 | C. |  | D. |  |
分析 求出原函数的导函数,由导函数的图象得到a>1,然后利用指数函数的图象平移得答案.
解答  解:∵$f(x)=\frac{1}{3}{x^3}+\frac{1}{2}(1-a){x^2}-ax+2$
解:∵$f(x)=\frac{1}{3}{x^3}+\frac{1}{2}(1-a){x^2}-ax+2$
∴f′(x)=x2+(1-a)x-a,
由函数y=f′(x)的图象可知$-\frac{1-a}{2}>0$,
∴a>1,
则函数g(x)=|ax-2|的图象是把函数y=ax向下平移2个单位,然后取绝对值得到,如图.
故可能是D.
故选:D.
点评 本题考查指数式的图象平移,考查了导数的综合运用,是中档题.

练习册系列答案
相关题目
14.以下关于x(x≥0)的不等式ln(x+1)+kx2-x≥0的结论中错误的是( )?
| A. | $?k≤\frac{1}{4}$,使不等式恒成立 | B. | $?k≥\frac{1}{4}$,使不等式恒成立 | ||
| C. | $?k≤\frac{1}{2}$,使不等式恒成立 | D. | $?k≥\frac{1}{2}$,使不等式恒成立 |
18.已知全集U={x|-1<x<3},集合A={x|x2-3x<0},则∁UA=( )
| A. | {x|-1<x≤0} | B. | {x|-1<x<3} | C. | {x|0<x<3} | D. | {x|x≤0或x≥3} |
15. 甲、乙两厂生产的一批零件尺寸服从N(5,0.12),如果零件尺寸在(μ-3σ,μ+3σ)以外,我们就有理由认为生产中可能出现了异常情况.现从甲、乙两厂各抽取10件零件检测,尺寸如茎叶图所示:则以下判断正确的是( )
甲、乙两厂生产的一批零件尺寸服从N(5,0.12),如果零件尺寸在(μ-3σ,μ+3σ)以外,我们就有理由认为生产中可能出现了异常情况.现从甲、乙两厂各抽取10件零件检测,尺寸如茎叶图所示:则以下判断正确的是( )
 甲、乙两厂生产的一批零件尺寸服从N(5,0.12),如果零件尺寸在(μ-3σ,μ+3σ)以外,我们就有理由认为生产中可能出现了异常情况.现从甲、乙两厂各抽取10件零件检测,尺寸如茎叶图所示:则以下判断正确的是( )
甲、乙两厂生产的一批零件尺寸服从N(5,0.12),如果零件尺寸在(μ-3σ,μ+3σ)以外,我们就有理由认为生产中可能出现了异常情况.现从甲、乙两厂各抽取10件零件检测,尺寸如茎叶图所示:则以下判断正确的是( )| A. | 甲、乙两厂生产都出现异常 | B. | 甲、乙两厂生产都正常 | ||
| C. | 甲厂生产正常,乙厂出现异常 | D. | 甲厂生产出现异常,乙厂正常 |
13.如图是某样本数据的茎叶图,则该样本的中位数、众数、极差分别是( )


| A. | 32 34 32 | B. | 33 45 35 | C. | 34 45 32 | D. | 33 36 35 |