题目内容
8.已知数列{an}满足a1=1,a2=2,$\frac{{{a_{n+2}}}}{a_n}$=3,则当n为偶数时,数列{an}的前n项和Sn=$\frac{3}{2}$(${3}^{\frac{n}{2}}$-1).分析 通过递推公式及前两项的值可知数列{an}中奇数项构成以1为首项、3为公比的等比数列,偶数项构成以2为首项、3为公比的等比数列,进而利用等比数列的求和公式计算即得结论.
解答 解:∵a1=1,a2=2,$\frac{{{a_{n+2}}}}{a_n}$=3,
∴数列{an}中奇数项构成以1为首项、3为公比的等比数列,
偶数项构成以2为首项、3为公比的等比数列,
∴数列{a2n-1+a2n}构成以3为首项、3为公比的等比数列,
又∵n为偶数,
∴Sn=$\frac{3(1-{3}^{\frac{n}{2}})}{1-3}$=$\frac{3}{2}$(${3}^{\frac{n}{2}}$-1),
故答案为:$\frac{3}{2}$(${3}^{\frac{n}{2}}$-1).
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
16.已知复数z满足z=$\frac{1}{2}$-i,$\overrightarrow{z}$为z的共轭复数,则(z-$\overrightarrow{z}$)2016等于( )
| A. | 22016 | B. | -22016 | C. | 22016i | D. | -22016i |
3.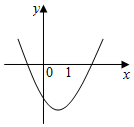 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )| A. | 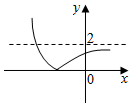 | B. | 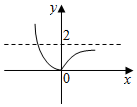 | C. |  | D. |  |
13.已知i是虚数单位,则i(1-i)2=( )
| A. | 2-2i | B. | 2+2i | C. | -2 | D. | 2 |
20.已知集合A={x|$\frac{x-2}{x}$≤0},B={x|-2≤x≤1},则A∩B=( )
| A. | [0,1] | B. | (0,1) | C. | [0,1) | D. | (0,1] |
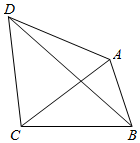 如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.
如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.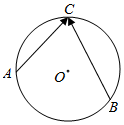 如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].
如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].