题目内容
12.设函数f(x)=|x+1|+|x-2|(Ⅰ)求f(x)的最小值,并求出f(x)取最小值时x的取值范围;
(Ⅱ)若不等式f(x)≤a(x+1)的解集为空集,求实数a的取值范围.
分析 (Ⅰ)采用零点分段法解含绝对值的不等式;( II)作出f(x)图象,结合图象可得a的取值.
解答 解:(Ⅰ)采用零点分段法求解,
①当x≥2时,f(x)=x+1+x-2=2x-1≥3;
②当-1≤x<2时,f(x)=x+1-x+2=3;
③当x<-1时,f(x)=-x-1-x+2=-2x+1≥3;
∴f(x)的最小值是3,此时x∈[-1,2];
(Ⅱ)由(Ⅰ)得:f(x)的图象如图示: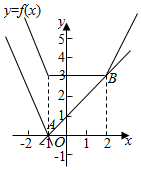
令g(x)=a(x+1),显然直线g(x)恒过(-1,0)点,
若不等式f(x)≤a(x+1)的解集为空集,
只需g(x)的图象(红色直线)和f(x)的图象(黑色线)无交点即可,
直线AB的斜率是:1,当x<-1时,f(x)=-x-1-x+2=-2x+1的斜率是-2,
故-2<a<1.
点评 本题考查绝对值不等式的解法及应用,数形结合是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.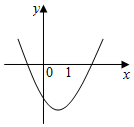 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )| A. | 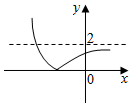 | B. | 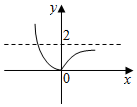 | C. |  | D. |  |
20.已知集合A={x|$\frac{x-2}{x}$≤0},B={x|-2≤x≤1},则A∩B=( )
| A. | [0,1] | B. | (0,1) | C. | [0,1) | D. | (0,1] |
7.已知实数x,y满足$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤a}\\{y≥-1}\end{array}\right.$,若z=2x+y的最大值为3,则实数a的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -$\frac{1}{2}$ |
4.已知F1(-3,0),F2(3,0),动点M满足|MF1|+|MF2|=5,则点M的轨迹是( )
| A. | 双曲线 | B. | 椭圆 | C. | 线段 | D. | 不存在 |
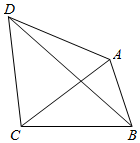 如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.
如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.