题目内容
14.以下关于x(x≥0)的不等式ln(x+1)+kx2-x≥0的结论中错误的是( )?| A. | $?k≤\frac{1}{4}$,使不等式恒成立 | B. | $?k≥\frac{1}{4}$,使不等式恒成立 | ||
| C. | $?k≤\frac{1}{2}$,使不等式恒成立 | D. | $?k≥\frac{1}{2}$,使不等式恒成立 |
分析 根据二次函数以及对数函数的性质判断即可.
解答 解:x≥0时,ln(x+1)≥0,
若不等式ln(x+1)+kx2-x≥0恒成立,
只需kx2-x≥0恒成立,
k=0时,不成立,
k≠0时,△=1-4k≤0,解得:k≤$\frac{1}{4}$,
故A、C、D正确,B错误.
故选:B.
点评 本题考查了函数恒成立问题,考查二次函数以及对数函数的性质,是一道中档题.

练习册系列答案
相关题目
9.若复数${z_1}={i^3}$,$\overline{z_2}=2+i$,则z1z2=( )
| A. | -1-2i | B. | -1+2i | C. | 1+2i | D. | 1-2i |
3.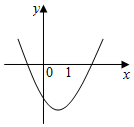 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
 已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )
已知a是常数,函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(1-a)x2-ax+2的导函数y=f′(x)的图象如图所示,则函数g(x)=|ax-2|的图象可能是( )| A. | 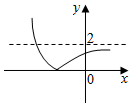 | B. | 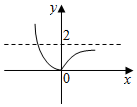 | C. |  | D. |  |
4.已知F1(-3,0),F2(3,0),动点M满足|MF1|+|MF2|=5,则点M的轨迹是( )
| A. | 双曲线 | B. | 椭圆 | C. | 线段 | D. | 不存在 |