题目内容
14.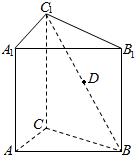 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.( I)若P为AB的中点,求证:DP∥平面ACC1A1;
( II)若$AP=\frac{1}{2}$,求三棱锥A-DCP的体积.
分析 (1)连接DP,AC1,由中位线定理可得DP∥AC1,故DP∥平面ACC1A1;
(2)由D为C1B的中点可知D到底面的距离为$\frac{1}{2}$AA1,求出△ACP的面积,代入体积公式计算即可.
解答 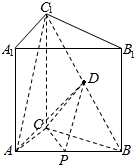 解:(1)证明:连接DP,AC1,
解:(1)证明:连接DP,AC1,
∵D为C1B的中点,P为AB的中点,
∴DP∥AC1,又∵AC1?平面ACC1A1,DP?平面ACC1A1,
∴DP∥平面ACC1A1.
(2)${S_{△ACP}}=\frac{1}{2}AC•AP•sin{60°}=\frac{{\sqrt{3}}}{4}$,
∵D是BC1的中点,∴D到平面ABC的距离h=$\frac{1}{2}$AA1=$\frac{3}{2}$.
∴V棱锥A-DCP=V棱锥D-ACP=$\frac{1}{3}$S△ACP•h=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{3}{2}$=$\frac{\sqrt{3}}{8}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
8.在正三棱柱ABC-A1B1C1中,已知AB=2,D是棱BB1的中点,且BD=1,则C1与平面ADC的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
3.从空间一点P向二面角α-L-β的两个面α,β分别作垂线PE,PF,E、F为垂足,若∠EPF=30°,则二面角α-L-β的平面角的大小是( )
| A. | 30° | B. | 150° | C. | 30°或150° | D. | 不确定 |
 中,四边形
中,四边形 是正方形,正三角形
是正方形,正三角形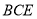 的边长为2,
的边长为2,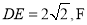 为线段
为线段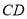 上一点,
上一点,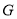 为线段
为线段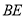 的中点.
的中点.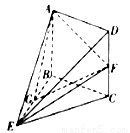
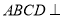 平面
平面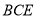 ;
;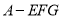 的体积.
的体积.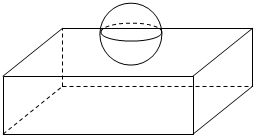 “80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R:
“80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R: